Question #a7296
1 Answer
Explanation:
We know that angular momentum
#vecL=vecrxxvecp#
where#vecp# is linear momentum and#=mvecv#
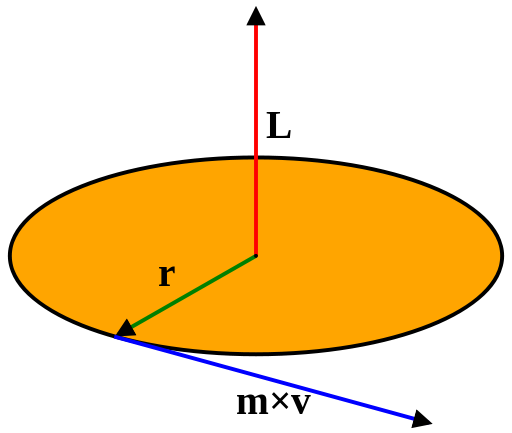
The velocity of the particle changes continuously due to acceleration due to gravity
Similarly horizontal component of velocity
We know that at maximum height vertical component of velocity is zero.
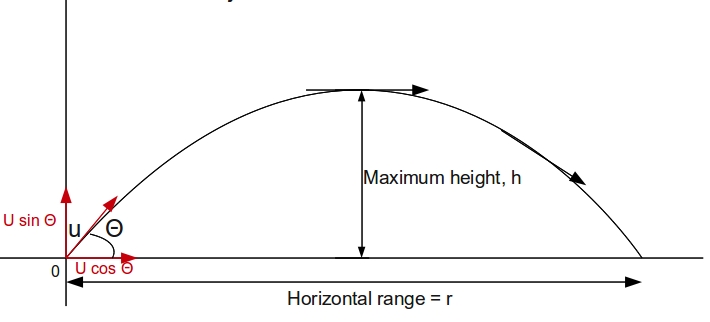
(Please read initial velocity as
Using the kinematic equation
Now
Inserting calculated values we get
