The line we are trying to find is perpendicular to #y=5#, which is a horizontal line.
The line which is perpendicular (at #90^o#) to a horizontal line is a vertical line, which would have the equation #x= "number"#. SO if we were to put any line which has the general equation #x= "number"#, the line should be perpendicular to #y=5#
Let's try this for #x=9#:
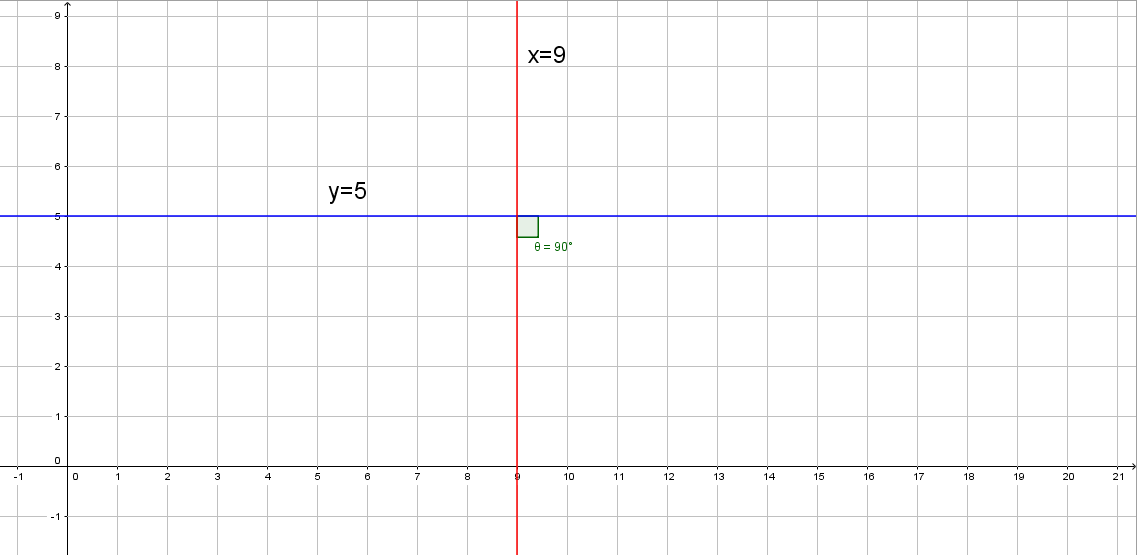
As you can, the angle between the two lines is #90^o#, hence #x=9# is perpendicular to #y=5#
One thing you should notice about any vertical line is that the #x#-coordinate is always the number that #x# equals in the equation. So with #x=9#, all the points will have an #x#-coordinate of 9.
Since we need the vertical line to go through #(-6,1)#, which has #x#-coordinate #-6#, the vertical line equation would be #x=-6#
If we graph this, it would look like:
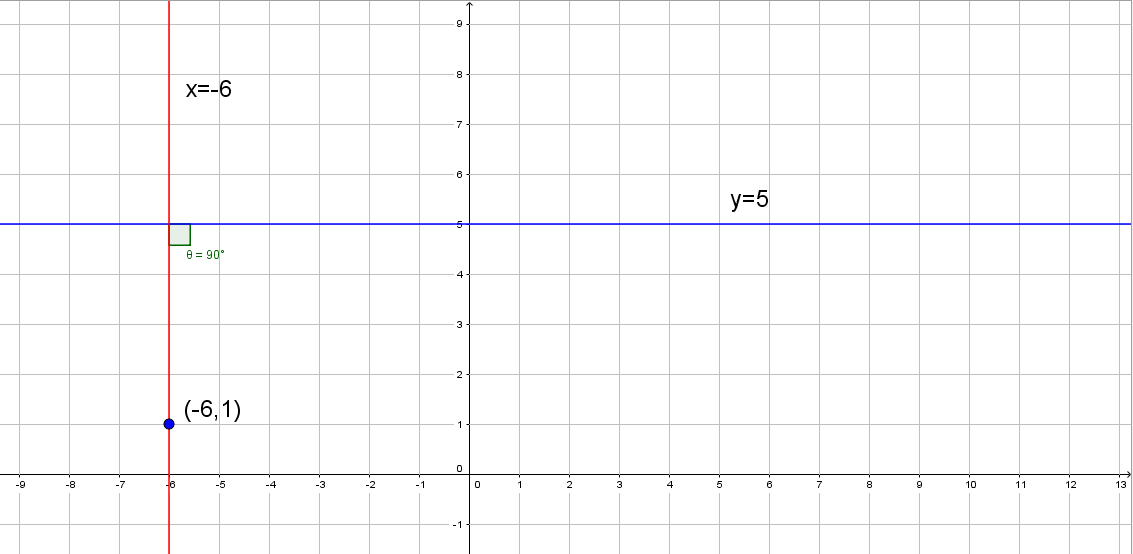
#x=-6# is perpendicular to #y=5# and also goes through the point #(-6,1)#, so this is your answer.
All lines with the general equation #x= "number"#, will not intercept the #y#-axis, hence they will not have #y#-intercepts. But, as mentioned before, all points will have an #x#-coordinate of the number given, so the #x#-intercept will also be the number given. As the equation of our line is #x=-6#, the #x#-intercept is #-6#.

