Show that the trajectory of a particle that is launched at an angle is parabolic?
1 Answer
For Physics or Mechanics you should learn the "suvat" equations for motion under constant acceleration:
#{: (v=u+at, " where ", s="displacement "(m)), (s=ut+1/2at^2, , u="initial speed "(ms^-1)), (s=1/2(u+v)t, , v="final speed "(ms^-1)), (v^2=u^2+2as, , a="acceleration "(ms^-2)), (s=vt-1/2at^2, , t="time "(s)) :} #
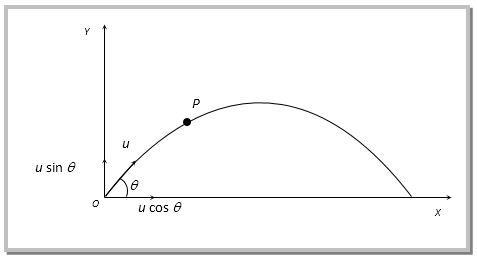
Consider a projectile launched at an angle
Horizontal Motion
The projectile will move under constant speed (NB we can still use "suvat" equation with a=0).
The projectile will travel a distance
# { (s=,x,m),(u=,u cos theta,ms^-1),(v=,"Not Required",ms^-1),(a=,0,ms^-2),(t=,t,s) :} #
So applying
# x = u \ costheta \ t#
Vertical Motion
The projectile travels under constant acceleration due to gravity. Considering upwards as positive, and again resolving the initial speed (vertically this time):
# { (s=,y,m),(u=,u sin theta,ms^-1),(v=,"Not Required",ms^-1),(a=,-g,ms^-2),(t=,t,s) :} #
Applying
# y = u \ sin theta \ t+1/2(-g)t^2#
# \ \ = u \ sin theta \ t - 1/2 g t^2#
Substituting for
# y = u \ sin theta \ (x/(u cos theta)) - 1/2 g (x/(u cos theta))^2#
# \ \ = (tan theta) x - g/(2u^2 cos^2 theta) \ x^2#
# \ \ = a x - b x^2 \ \ # , say, where#a,b# are constants.
Which is the trajectory of a parabola.

