Question

Question #59194

Answer 1

As explained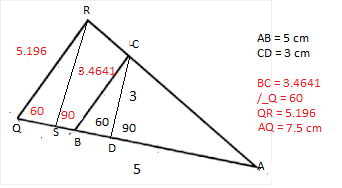

Explanation:

Since triangles ABC & AQR are similar,

`(AQ )/ (AB) = (AR) / (AC) = (QR) / (BC)`

Also `AhatBC = AhatQR = 60^0`

But AQ = AB * 1.5 = 5 * 1.5 = 7.5 cm#

From the diagram,
BC = (CD) / sin 60 = 3 / (sqrt3/2) = 2 sqrt3 = 3.4641#

QR = (BC) * 1.5 = 3.4641 * 1.5 = 5.196 cm#

Now we know two sides AQ, QR and included angle `hatQ`

Now we can construct `Delta AQR`

Answer 2

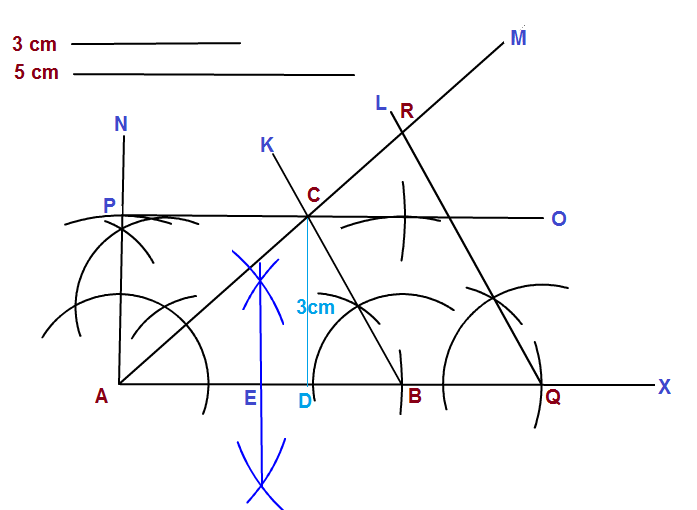
Steps for construction

1. Line segments of length 5cm and 3cm are drawn with the help of a ruler.
2. A line segment `AX` of length `> 8cm` is also drawn similarly.
3. Line segment `AB` is then cut off from AX with the help of a compass.
4. `/_ABK=60^@` is drawn with the help of a ruler and a compass.
5. With the help of a ruler and a compass a perpendicular `AN` on `AB` at `A` is drawn and an intercept `AP=3cm` is cut off with the help of a compass.
6. `PO` is drawn parallel to `AB` with the help of a compass and a ruler. `PO` intersects `BK` at `C`. `A and C` are joined . The `DeltaABC` is the required triangle having altitude `CD=3cm`.
7. `AB` is bisected at `E` with the help of a compass and a ruler.
8. Line segment `BQ=BE` is cut off from extended part of `AB` to make `AQ=1.5xxAB`.
9. `/_AQL=60^@` is drawn to get get `QL"||"BC`. This QL intersects extended `AC` at `R`.
10. Now `DeltaAQR` is the similar to `DeltaABC` having `1.5` times of the corresponding sides of `DeltaABC`.