Question

Question #7f0f6

Answer 1

`"the equation of the line is -2 x+3 y=13 or "y=2/3 x+13/3`

Explanation:

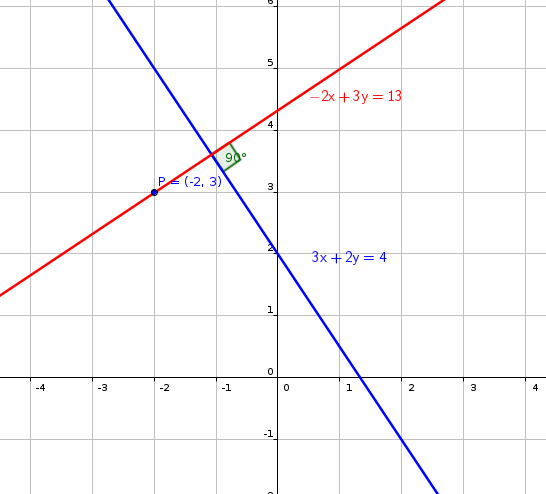
`color(blue)(2y+3x-4=0)" the equation of the blue line"`

`"let's rearrange the equation of the blue line"`

`color(blue)(2y=-3x+4)`

`color(blue)(y=-3/2 x+2) " (1)"`

`y=m x+n " represents the standard form of the line"`

`"where m is slope of line"`

`m=-3/2`

`"let the slope of the red line perpendicular to the blue line be " m_1`

`m*m1=-1`

`-3/2*m_1=-1`

`m_1=2/3`

`"now we can use the slope-intercept form of the equation of line"`
`color(red)(y-y_1=m(x-x_1)`

`color(red)(y-3=2/3(x+2))`

`color(red)(y-3=2/3 x+4/3)`

`color(red)(y=2/3 x+4/3+3)`

`color(red)(y=2/3 x+13/3)`

`"or "`

`"let's multiply both sides of equation by 3"`

`3y=2x+13`

`-2x+3y=13`