We could do this with a memorized formula (skip to the end for the general formula), but here it is in a somewhat detailed form:
We are interested in the area bounded by
#color(white)("XXX")color(red)(y=4-x^2)#
and the X-axis (where #y=0#) and the Y-axis.
(Note that #y=4-x^2# crosses the positive X-axis at #x=2#)
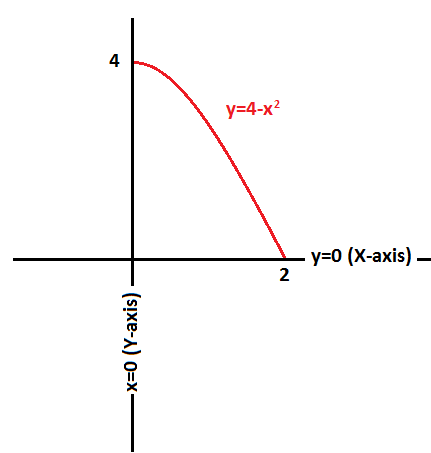
If we start by considering the #color(green)("Area")# of a circle formed by rotating #color(red)(y=4-x^2)# for any arbitrary point #color(green)x in [0,2]#
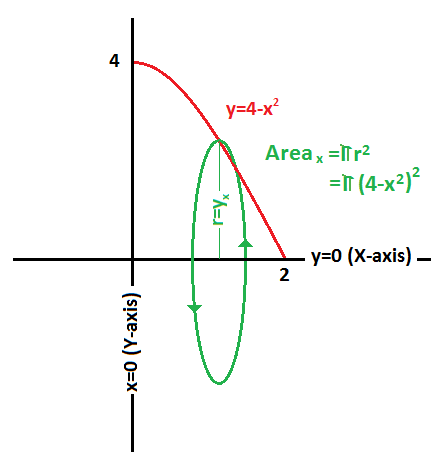
Then if we consider a thin disk with a thickness of #color(blue)(dx)# formed from this circular area:
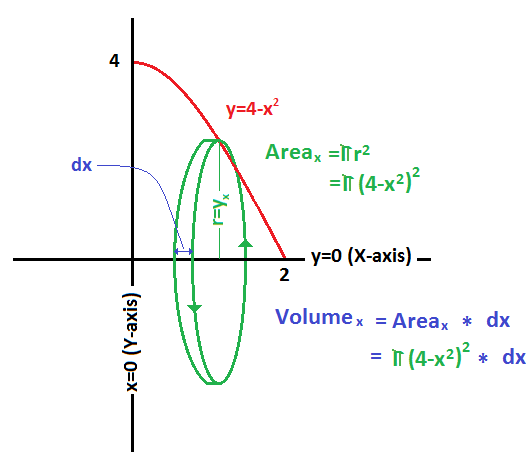
We can (hopefully) see that provided #color(blue)(dx)# is small, the sum of all such disk volumes will be close to the volume of the entire rotated function.
In fact, it would be reasonable to claim that the volume of the rotated image of #y=4-x^2# is
#color(white)("XXX")lim_(dxrarr0) Sigma_(x=0,"step:"dx)^2color(white)("xx") pi(4-x^2)^2#
[Take a moment to consider this.]
This is, of course, just an expansion of the normal notation:
#color(white)("XXX")int_0^2 pi(4-x^2)^2 dx#
Expanding #(4-x^2)^2# to #x^4-8x^2+16#
and then taking the indefinite integral:
#color(white)("XXX")int_0^2 pi(x^4-8x^2+16) =pi((x^5)/5-(8x^3)/3+16x+C)#
We have the required volume:
#color(white)("XXX")pi((x^5)/5-(8x^3)/3+16x)|color(white)(uarr)_color(brown)0^color(magenta)2#
#color(white)("XXX")=color(magenta)(pi(32/5-64/3+32))-color(brown)(pi(0-0+0))#
#color(white)("XXX"256/15 pi#
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
...and here is the promised general formula for a function #f(x)# bounded by the Y-axis and rotated about the positive X-axis:
#color(white)("XXX")"Vol"=int_0^a pi(f(x))^2 dx#
where #a# is the x-intercept.
If you followed through with the example, the reason for this general formula should be clear.



