Question #aa5c1
1 Answer
Mar 3, 2017
Explanation:
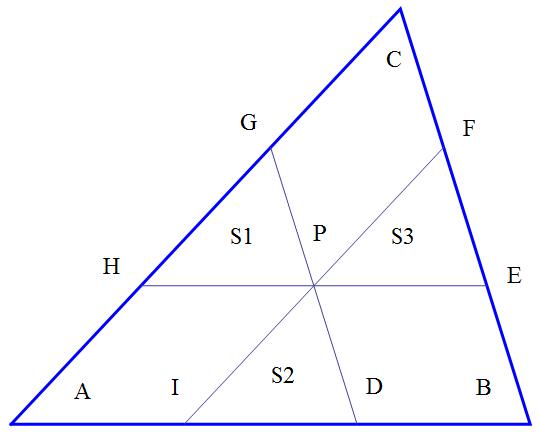
Let
by similarity of triangles we have
because in two similar triangles, the ratio of their areas is equal to the square of the ratio of their respective sides.
But
so
then
or

