Question #3d4ae
1 Answer
Explanation:
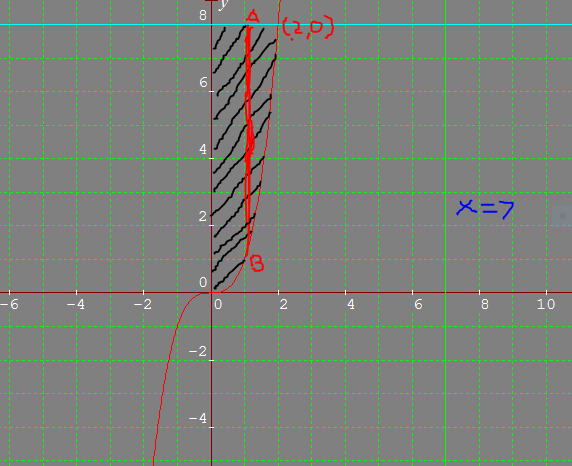
The region to be revolved around x=7 is shown shaded in black in the attached diagram. For this region x would vary from x=0 to x=2. Now consider an element of length AB(thickness dx ), of this region at a distance x from from y-axis. Length AB would be
Now if this element is rotated about x=7, the surface area of this cylindrical shell would be
The volume of the solid so generated by revolving the whole shaded region would then be
=
=
=