Find the vector equation of the line perpendicular to the vectors #3bb(ulhati)-4bb(ul hatj)+bb(ul hatk)# and #2bb(ul hatj)+3bb(ul hatk)#?
1 Answer
# bb(vecr) = ( (2), (1), (-1) )+ lamda ( (-14), (-9), (6) ) #
Explanation:
First consider the vectors
# bb(vecn) = ( (3), (-4), (1) ) xx ( (0), (2), (3) ) #
# \ \ \ \ = | (bb(ul hati), bb(ul hatj), bb(ul hatk)), (3,-4,1), (0,2,3) | #
# \ \ \ \ = | (-4,1), (2,3) | bb(ul hati) - | (3,1), (0,3) | bb(ul hatj) + | (3,-4), (0,2) | bb(ul hatk)#
# \ \ \ \ = (-12-2) bb(ul hati) - (9-0) bb(ul hatj) + (6-0) bb(ul hatk)#
# \ \ \ \ = -14 bb(ul hati) - 9 bb(ul hatj) + 6 bb(ul hatk)#
So now that we have the vector that the line is in the direction of, so the line equation is given by:
# bb(vecr) = bb(vec(OG)) + lamda bb(vecr) #
# \ \ \ \ = ( (2), (1), (-1) )+ lamda ( (-14), (-9), (6) ) #
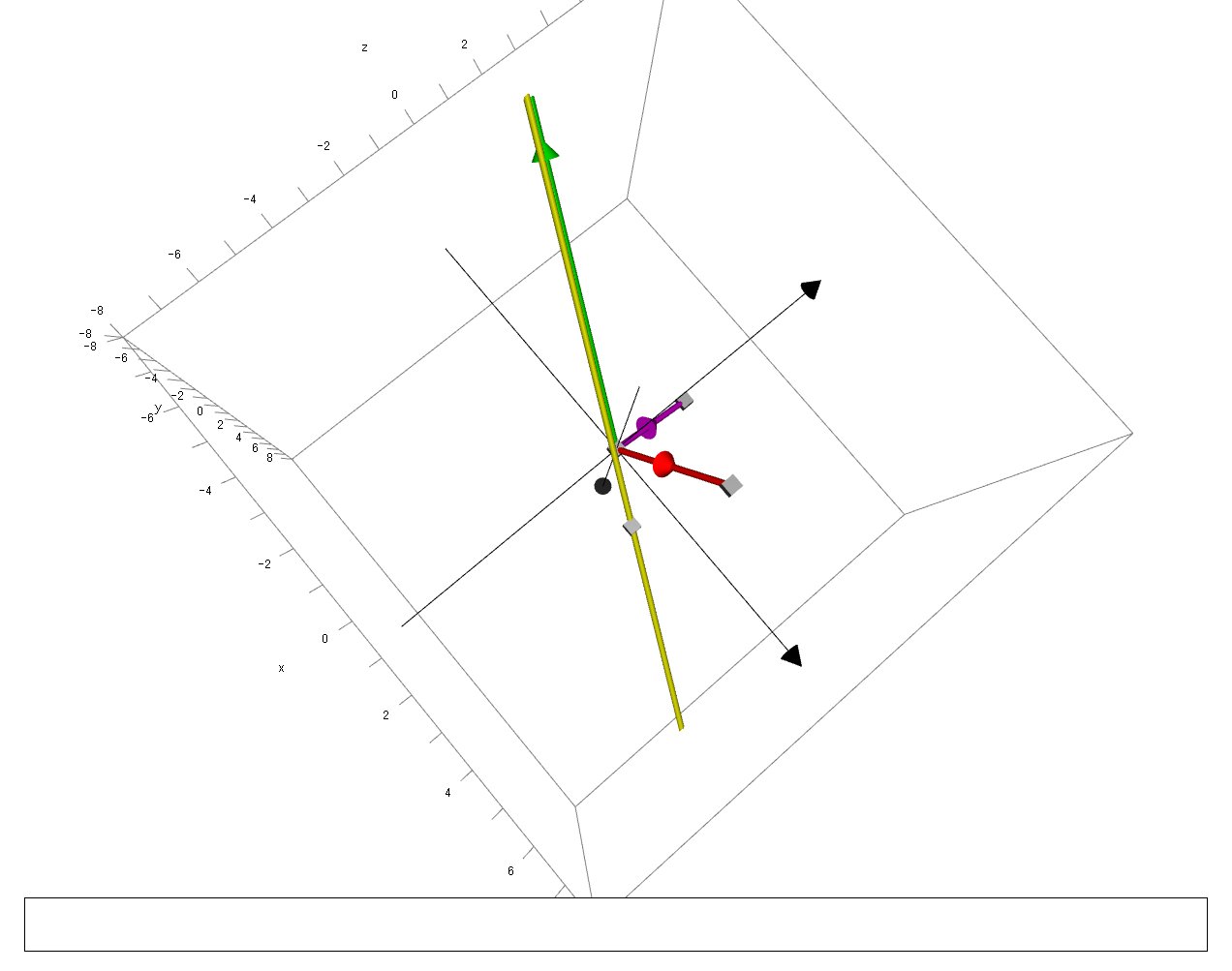
We can confirm this with a 3D diagram: