Question

Question #d772b

Answer 1

I tried this:

Explanation:

You have that an electron in jumping from one level to another (as in your case, going down) will release energy in form of a photon of light.
The energy correspondent to this jump can be evaluated using a formula from Bohr's Theory (you can find it in the part of Quantum Physics of your book near Bohr's Postulates or Hidrogen Spectrum or at http://hyperphysics.phy-astr.gsu.edu/hbase/hyde.html):
We start using:
`"Energy difference"=-13.6[1/n_1^2-1/n_2^2]` in `eV`

Where:
`n_1=2`
`n_2=4`
To get:
`"Energy"=-13.6[1/4-1/16]=-2.55eV` emitted during the transition.
For semplicity I now change it into Joules to get the usual units for frequency and wavelength:
I know that:
`1eV=1.6xx10^-19J`
so `2.55eV=4.1xx10^-19J`
I can get the frequency `f` knowing that for energy we have:
`E=hf` (where `h` is Planck's Constant)
so:
`f=E/h=(4.1xx10^-19)/(6.63xx10^-34)=6.2xx10^14Hz`
and for the wavelength `lambda`:
`lambda=c/f=(3xx10^8)/(6.2xx10^14)=4.851xx10^-7~~485nm`
By the way `c=3xx10^8m/s` is the speed of light in vacuum that will be the speed of your photon!

Answer 2

`sf((1))`

`sf(2.55color(white)(x)"eV")`

`sf((2))`

`sf(6.16xx10^(14)color(white)(x)"Hz")`

`sf((3))`

`sf(2.998xx10^(8)color(white)(x)"m/s")`

`sf((4))`

`sf(486.2color(white)(x)"nm")`

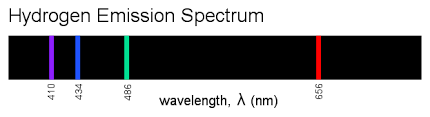
Explanation:

If you are working in electron volts then the energy of the electron in a particular energy level is given by:

`sf(E=(-13.6)/(n^2)" ""eV")`

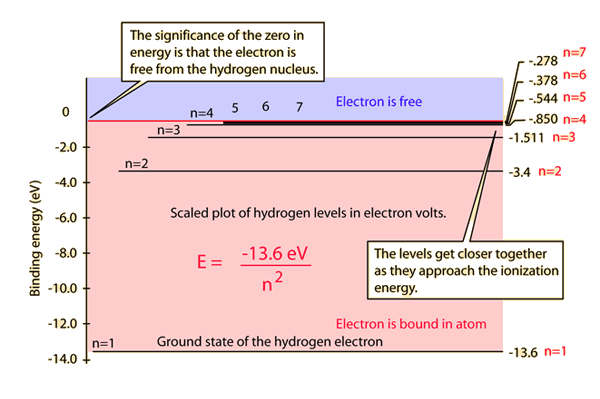
Where n is the principal quantum number.

When n = 2:

`sf(E=(-13.6)/(2^2)=-3.40color(white)(x)"eV")`

When n = 4:

`sf(E=(-13.6)/(4^2)=-0.850color(white)(x)"eV")`

This means the transition energy will be the difference between the 2 values:

`sf(DeltaE=-0.850-(-3.40)=2.55color(white)(x)"eV")`

`sf((2))`

The electron volt is not the standard unit for energy so we must convert it to Joules. To do this we multiply by the electronic charge:

`sf(E=2.55xx1.602xx10^(19)" "J)`

`sf(E=4.085xx10^(-19)" "J)`

To find the frequency f we use the Planck Expression:

`sf(E=hf)`

Where h is the Planck Constant.

`:.` `sf(f=E/h)`

`sf(f=(4.085xx10^(-19))/(6.626xx10^(-34))=6.165xx10^(14)" ""Hz")`

`sf((3))`

The photon will travel at the speed of light c . This is a universal constant:

`sf(c=2.998xx10^8color(white)(x)"m/s")`

`sf((4))`

The relationship we need is :

`sf(c=flambda)`

`:.` `sf(lambda=c/f=(2.998xx10^(8))/(6.165xx10^(14))=0.4862xx10^(-6)" "m)`

`sf(lambda=486.2color(white)(x)nm)`