Question

Question #d0643

Answer 1

`79/93`

Explanation:

The idea here is that ideally, iron(II) oxide is made up of iron(II) cations, `"Fe"^(2+)`, and oxide anions, `"O"^(2-)`, present in a `1:1` ratio in the compound's lattice structure.

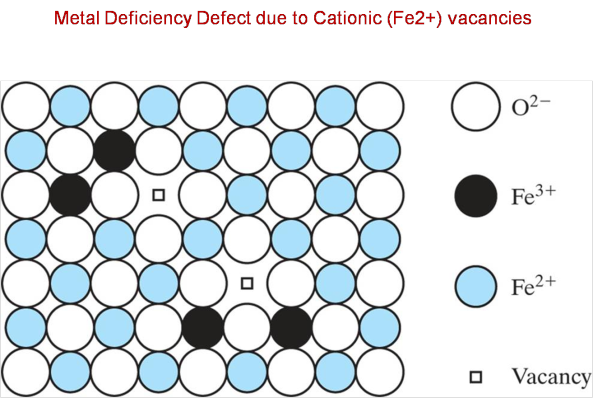
However, it is quite common to have cases where some of the iron(II) cations are missing from the lattice structure `->` this is known as a metal deficiency defect.

In order for the overall positive charge to balance the overall negative charge, i.e. in order to continue to have a neutral compound, some of the remaining iron(II) cations are oxidized to iron(III) cations, `"Fe"^(3+)`.

More specifically, for every iron(II) cation that is missing from the lattice structure, two iron(II) cations are being oxidized to iron(III) cations.

Now, `"Fe"_0.93"O"_1`, which is a form of the mineral wustite, contains iron(II) cations and oxide anions in a `0.93:1` ratio.

Since it's easier to work with whole numbers, you can say that for every `100` `"O"^(2-)` anions, the lattice structure contains `93` `"Fe"^(2+)` cations.

In other words, for every `100` `"O"^(2-)` anions, `7` `"Fe"^(2+)` cations are missing from the lattice structure.

Since you know that for every missing iron(II) cation, two iron(II) cations must be oxidized to two iron(III) cations in order for the positive charge of the cations to continue to balance the negative charge of the anions, you can say that this lattice structure will contain

`overbrace(2 xx "7 Fe"^(2+))^(color(blue)("2 for every missing Fe"^(2+))) = "14 Fe"^(3+)`

This means that out of every `93` cations that are present for every `100` oxide anions, the lattice structure will contain

• `"14 Fe"^(3+)` `"cations"`
• `93 - 14 = "79 Fe"^(2+)` `"cations"`

Therefore, the fraction of iron(II) cations that you get for every `100` oxide anions is equal to

`(79 color(red)(cancel(color(black)("Fe"^(2+)color(white)(.)"cations"))))/(93 color(red)(cancel(color(black)("cations")))) = 79/93`