How do the chemical potentials compare for the vapour and liquid phases at, below, and above the boiling point in a phase diagram?
2 Answers
The chemical potentials are the same for the vapour phase and the liquid phase when we are at the boiling point exactly.
Explanation:
Chemical potential is a form of potential energy that can be absorbed or released during a chemical reaction or phase transition.
Assume that you have a container of water.
Above 100 °C, a water molecule that is in the vapour phase has a lower chemical potential than one that is in the liquid phase.
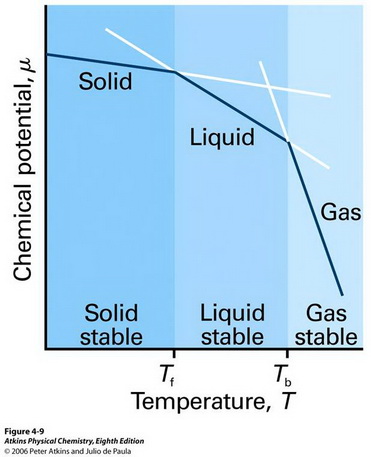
(From chem331001fall09.pbworks.com)
Water molecules in the liquid phase convert to gas, where their chemical potential is lower, so the water evaporates.
Below 100 °C, the molecules in the liquid phase have the lower chemical potential, so the vapour condenses to liquid.
At 100 °C the chemical potentials in liquid and vapour are the same, and the system is at equilibrium.
Here's another way to look at this.
The chemical potential
#mu = G/n# where
#G# is a function of temperature#T# and pressure#P# in a thermodynamically-closed system (conservation of mass and energy).
Let
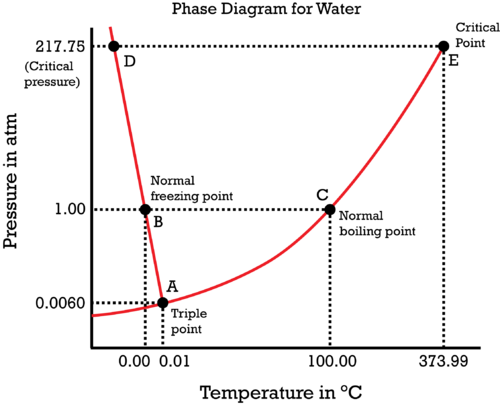
#(1)" "# At the boiling point (for a given pressure), the liquid and vapor phases are in phase equilibrium with each other, i.e. they are at constant temperature and pressure and exist at the same time. So,#mu_((g)) = mu_((l))# , or#Deltamu = 0# .
#(1)# would be the case at point#"C"# . If we decrease the pressure at constant temperature, we favor the vapor phase (by moving downwards on the phase diagram, off of#bar(AC)# ), so that#mu_((g)) < mu_((l))# .
#(2)" "# Below the boiling point (for a given pressure), the liquid phase is favored (as we're not boiling), so#mu_((l)) < mu_((g))# .
#(2)# would be the case directly to the left of point#"C"# . Increasing the temperature at constant pressure would increase#mu_((l))# and decrease#mu_((g))# until we reach the boiling point (at which#mu_((g)) = mu_((l))# ).
#(3)" "# Above the boiling point (for a given pressure), the vapor phase is favored (as we're past boiling), so#mu_((g)) < mu_((l))# .
#(3)# would be the case directly to the right of point#"C"# . Decreasing the temperature at constant pressure would decrease#mu_((l))# and increase#mu_((g))# until we get back down to the boiling point (at which#mu_((g)) = mu_((l))# ).


