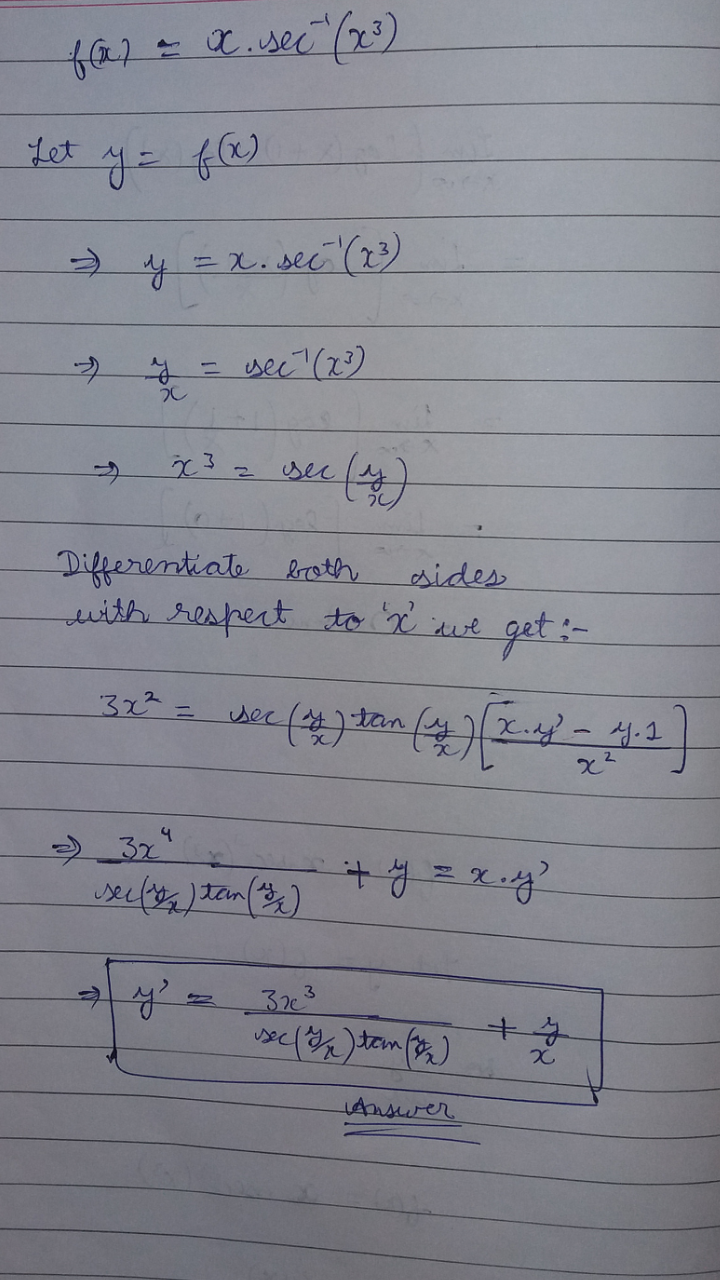Question #2cc56
3 Answers
Use the product rule and the chain rule.
Explanation:
Given:
The product rule is:
For the given function:
Let
The computation of
Let
Substitute these into the right side of the chain rule:
Reverse the substitution for h:
Two powers of x cancel and the 3 can move to the numerator:
Returning to the product rule:
Substitute the values into the product rule:
one power of x cancels in the second term:

Explanation:
We know that differential of inverse trigonometric ratio
We get
Given expression is
Using chain rule we get
Using (1) we get