Question #61134
2 Answers
Apr 10, 2017
Ok, I hope I got the questions right...!
Explanation:
I will start from the second that helps to understand the first...
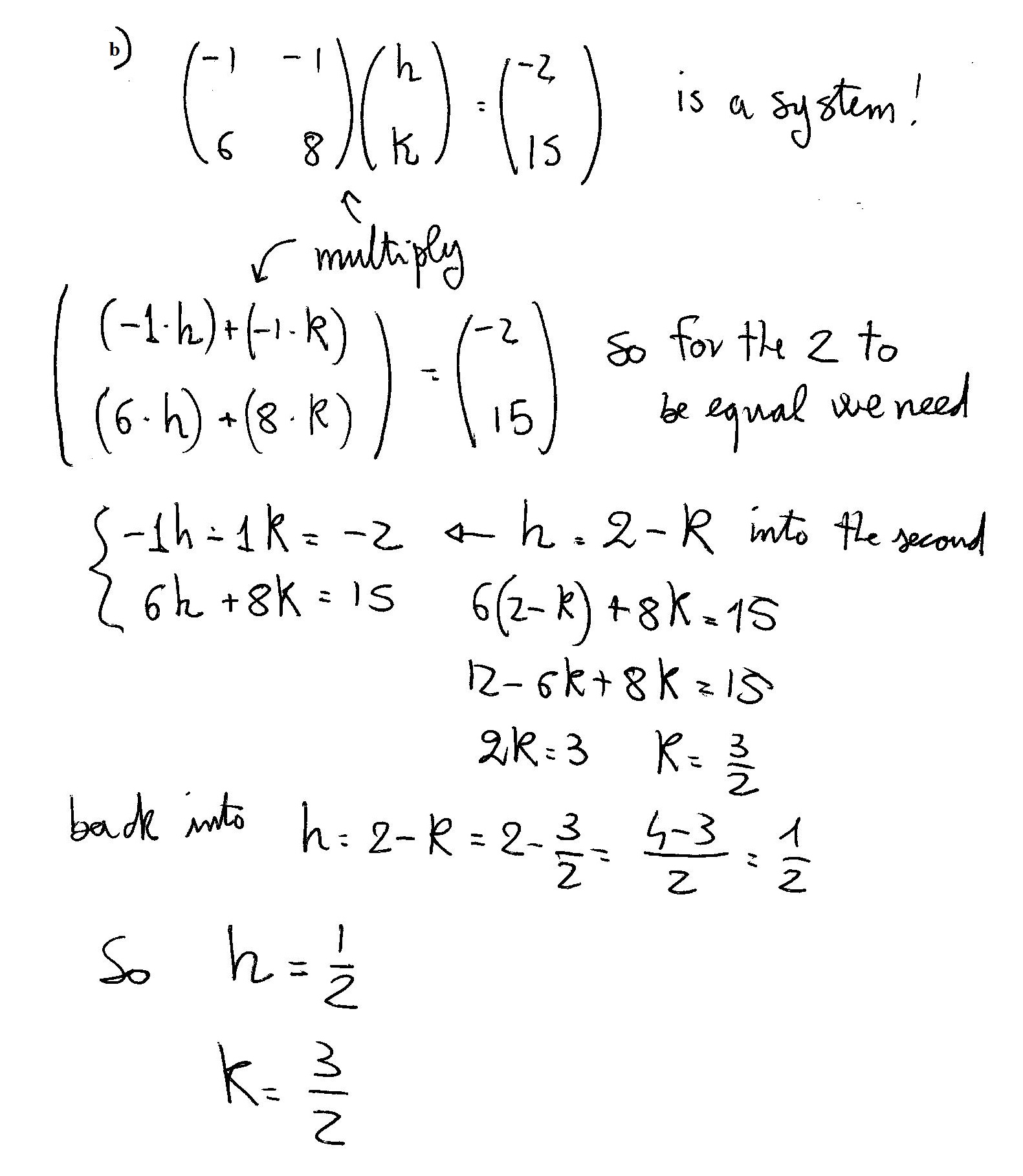
Now you can try to solve question a) where I think he wants the inverse:
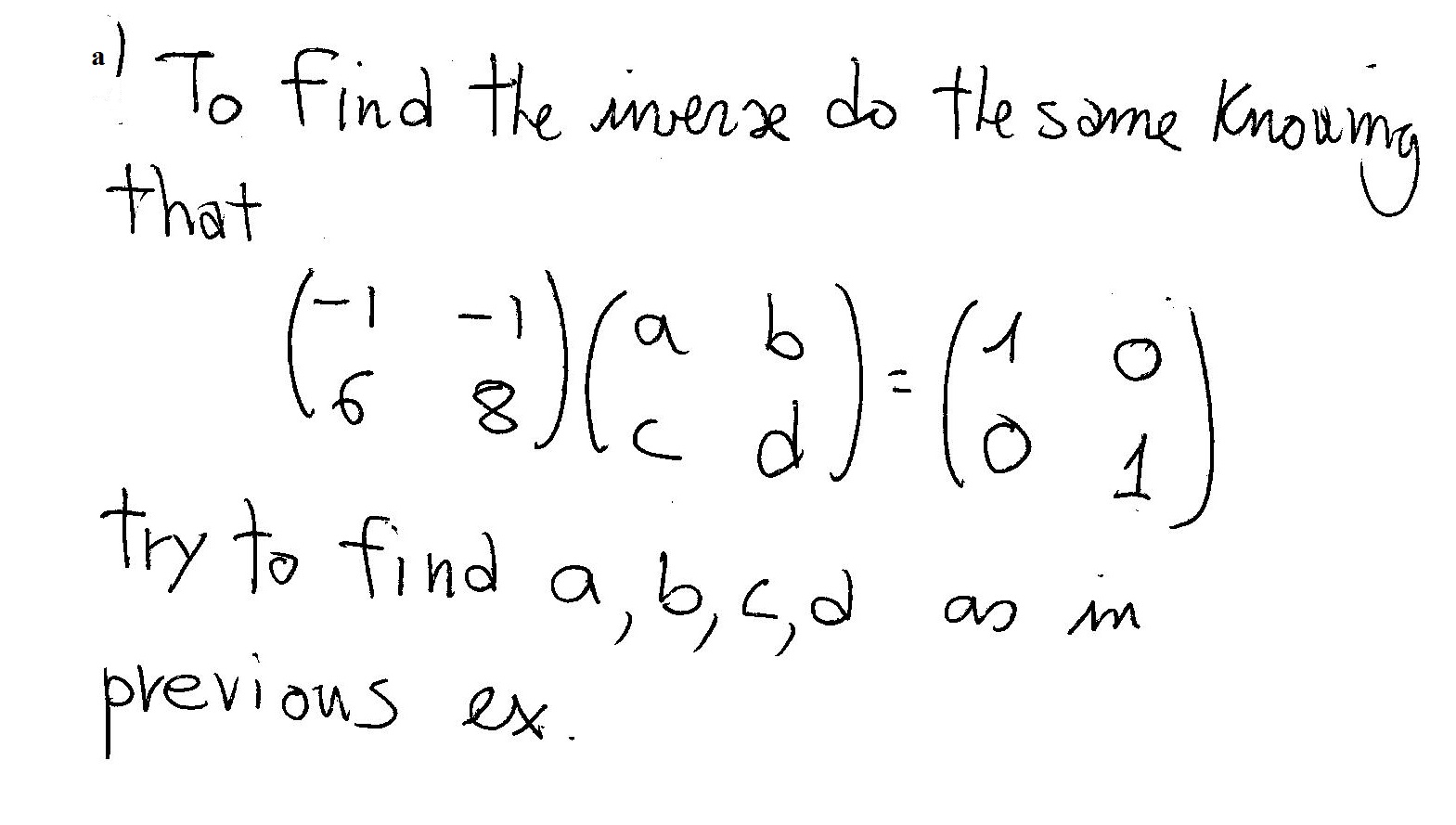
The matrix with
If you cannot find it let me know...:-)
Apr 10, 2017
ok then...let us try:
Explanation:
Have a look:


Now try by yourself to test the inverse doing:

