I think there might be something wrong with part (i) of your question.
Let's assume (taking a very specific case) in 2-D Cartesian:
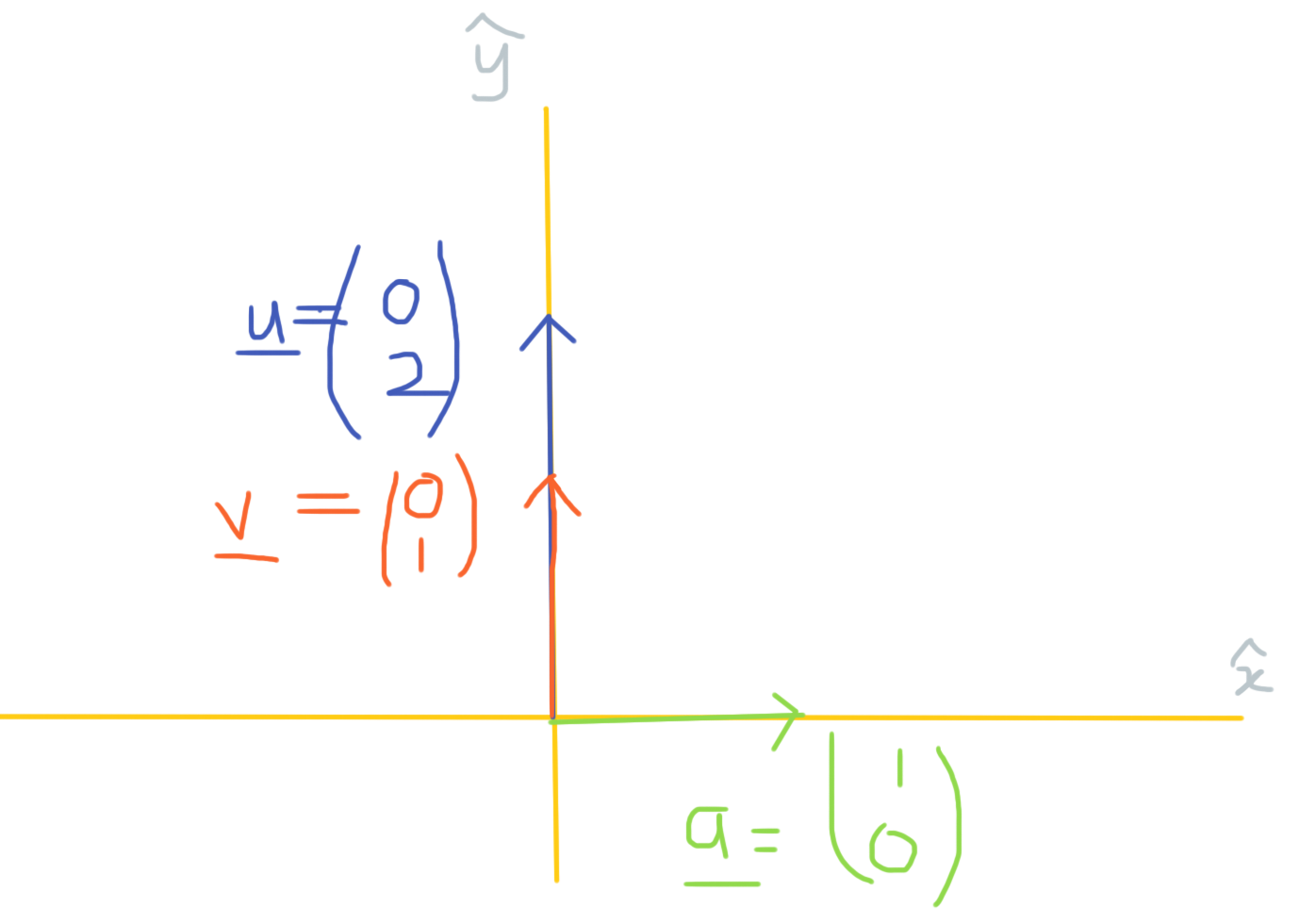
#vec u = (0,2)^T#, #vec v = (0,1)^T# and #vec a = (1,0)^T#
Assuming, in the usual course, that your notation means that:
#Proj_a vec u = Proj_a vec v implies vec u cdot hat a = vec v cdot hat a#
...where #hat a# is the unit #vec a# vector , then we have:
# vec u cdot hat a = (0,2)((1),(0)) = 0#
# vec v cdot hat a = (0,1) ((1),(0)) = 0#
So #Proj_a vec u = Proj_a vec v = 0#, which is your requirement in this very specific case.
But:
#vec u cdot vec v = (0,2)((0),(1)) = 2#
And:
#vec v cdot vec a = (0,1)((1),(0)) = 0#
So:
#vec u cdot vec v ne vec v cdot vec a #
The second bit (ie: part(ii)) is actually a lot easier to show once you add on the necessary conditions.


