Question

Question #c6184

Answer 1

`C=27.1^@` or `C=153^@`

Explanation:

This question concerns itself with the ambiguous case of the sine rule.
Sometimes with the sine rule, you can get two values for the angle. One is acute, the other is obtuse.
This is partly because there are two triangles we can draw for the information given:

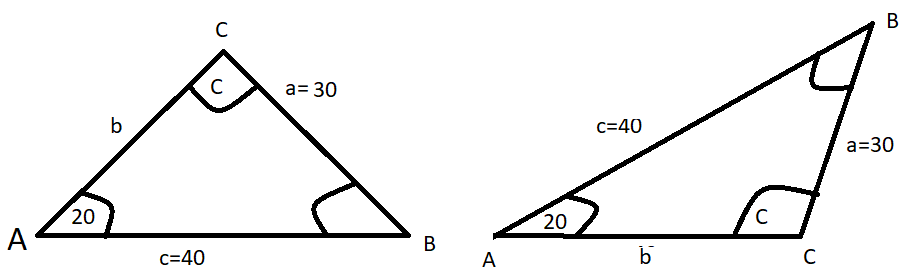
The way we calculate the angle is the same regardless. We use the sine rule:

`sinA/a=sinC/c`.

`sinC=(csinA)/a`

`sinC=(40sin20)/30`

`sinC=0.45602...`

Leave this value in your calculator.

One of the answers for the angle will be the inverse sine of this.

`C=27.131...`
`C=27.1^@`

C can also be `180-C`, (I will show why later).

so `C=180-27.131...`
`C=152.868...`
`C=153^@`

So why does this work? Consider the graph of `y=sinx` for `0^@<=x<=180^@`

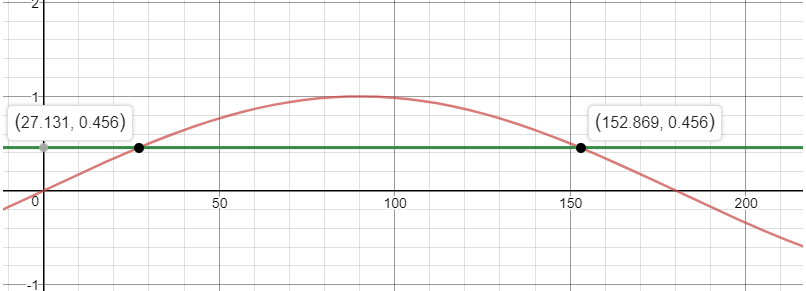
The red curve is the graph of `y=sinx`, and the green line is the line `y=4/3sin20`, which is what we obtained from the sine rule earlier.

Since we know that our angle is in a triangle, it cannot be greater than 180, and cannot be less than 0.

However, in this range, note how there are two solutions to these equations? One at `27.131^@,` and one at `153.869^@`. This means that our angle C can take either of these values, whether it is acute or obtuse.

For any angle, `theta, sintheta=sin(180-theta)`. It is necessary to consider both angles.

This does not arise for the cosine rule. The graph of `y=cosx` does not give the same value for the range `0<=x<=180`, so such a problem does not arise.