Question #78ef0
1 Answer
Apr 22, 2017
Explanation:
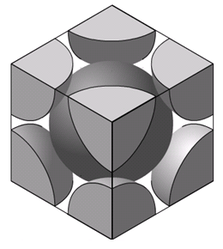
Body-Centered Cubic lattice structure is as shown in the figure. One atom is located at the lattice point at the center of the cube. Eight atoms are placed at eight lattice points located at the corners of the cube.
- The atoms touch each other along the directions of body diagonals.
- Only 1/8th of each atom in the corner belongs to the cell.
- The one in the center of the cell entirely belongs to the unit cell.
- As such there are 2 atoms per unit cell
Look at the geometry of the BCC structure as reproduced below:
Where
From Pythagoras theorem
And
#(4r)^2=d^2 + (dsqrt2)^2#
#=>(4r)^2=3d^2 #
#=>r=sqrt3/4d #
Inserting given value in above we get
atomic radius of the element
