Your goal here is to figure out if #"9.9 eV"# of energy are enough to excite a hydrogen atom in its ground state and if so, the highest energy level that the electron can reach.
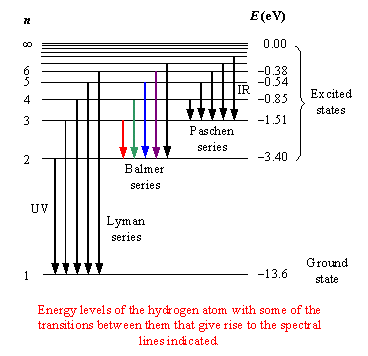
The easiest way you have of figuring out if #"9.9 eV"# is enough energy to bump the electron from the first energy level is to subtract the energy of the ground level, for which #n=1#, and the energy of the first excited state, for which #n=2#.
You will end up with--you can ignore the minus signs for this purpose
#"13.6 eV " - " 3.40 eV" = "10.2 eV"#
This tells you that in order for an electron to move from #n=1# to #n=2# in a hydrogen atom, it must absorb #"10.2 eV"# of energy.
Since you only have #"9.9 eV"# available, you can say that the electron won't absorb the energy needed for this transition to take place, which implies that the number of spectral lines emitted will be equal to #0#.
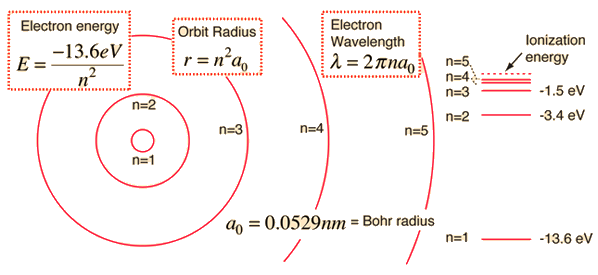
Alternatively, you can use the fact that the quantized energy levels that the electron can occupy in a hydrogen atom are described by the following equation
#E_n = -"13.6 eV"/n^2#
Here #n# represents the principal quantum number that describes a given energy level.
In your case, you will have
#E_n = -"13.6 eV" + "9.9 eV" = -"3.7 eV"#
This means that #n# will be
#n^2 = (color(red)(cancel(color(black)(-)))13.6 color(red)(cancel(color(black)("eV"))))/(color(red)(cancel(color(black)(-)))3.7color(red)(cancel(color(black)("eV")))) implies n= sqrt(13.6/3.7) ~~ 1.9#
Since you have #1 < n < 2#, you can conclude that the electron did not absorb enough energy to get to the second energy level #-># no spectral lines will be emitted.



