Question #17dc3
1 Answer
The compound is
Explanation:
This is an ionic compound. Because the anions are larger, they form the HCP array and the cations occupy the tetrahedral holes.
Let's start with a review of terms.
Hexagonal closest packing
Below is a diagram of an HCP unit cell.

There is
Tetrahedral holes
A tetrahedral hole is the space between four atoms that are touching each other.
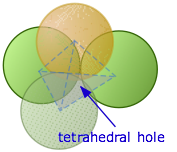
How many tetrahedral holes in an HCP unit cell?
For simplicity, let's examine just the parallepiped that makes up one-third of the unit cell.
(Adapted from OoCities)
Since this is one-third of a unit cell, it contains two atoms.
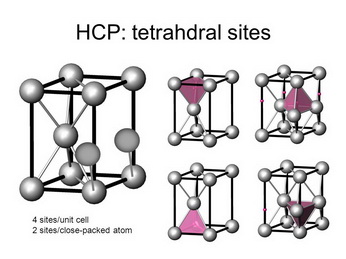
(From SlidePlayer)
There are four tetrahedral holes — or two for each atom.
The unit cell contains 6 atoms, so it contains 12 tetrahedral holes.
Formula of the compound
The unit cell contains 6 anions of
One-third of the holes contain cations of
Hence, the formula of the unit cell is
The empirical formula of the compound is

