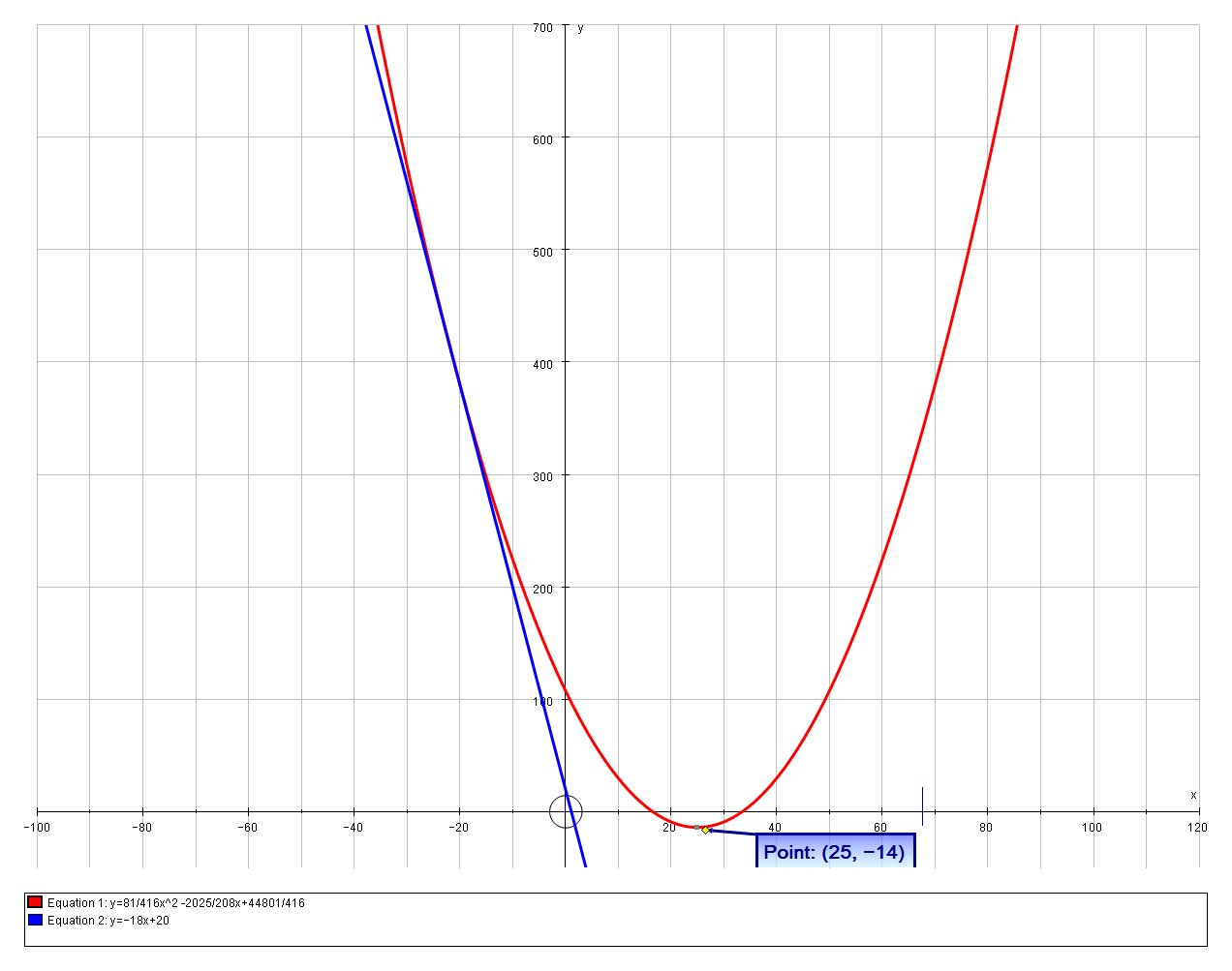
A parabola has a critical point at #(25, -14)#. It also has a tangent with equation #y=-18x+20 #. What is the equation of the parabola?

Question

1364 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-04-26T01:52:48

# y=81/416x^2 -2025/208x+44801/416#

Suppose the required parabola has the equation:

# y=ax^2+bx+c #

We differentiate wrt #x# to get the first derivative:

# y'=2ax+b #

We want a critical point at #(25, -14)#, so we can use #y'=0# at that point:

# x=25 => 2*25a+b = 0 #

# :. 50a+b = 0 => b=-50a#

This critical point #(25,-14)# also lies on the original curve:

# x=25 => 625a+25b+c=-14 #

# :. 625a+25(-50a)+c=-14 #
# :. 625a-1250a+c=-14 #
# :. 625a-c=14 => c=625a-14#

We also require one simultaneous solution of:

# y=ax^2+bx+c #
# y=-18x+20 #

So that:

# ax^2+bx+c = -18x+20 #
# :. ax^2+(b+18)x+c-20 = 0 #

For one solution then the discriminant must be zero:

# :. (b+18)^2 - 4(a)(c-20) = 0 #

Substituting #b=-50a# and #c=625a-14# gives:

# :. (-50a+18)^2 - 4a(625a-14-20) = 0 #
# :. 2500a^2 -1800a+324 -2500a^2+136a = 0 #
# :. -1664a+324 = 0 #
# :. a=81/416 #

And so:

# b=-2025/208#
# c= 44801/416#

Hence the equation we seek is

# y=81/416x^2 -2025/208x+44801/416#

We can validate the solution graphically:
enter image source here