Question #a6987
1 Answer
when the speeds of source and the receiver relative to the air are lower than the velocity of sound in the air, the relationship between observed frequency
#nu= (v+v_r)/(v+v_s)nu_0....[1]# ,
where
-
#v# is the velocity of sound in the air; -
#v_r# is the velocity of the receiver of sound relative to the air. It is positive if the receiver is moving towards the source and negative in the other direction; -
#v_s# is the velocity of the source relative to the air. It is positive if the source is moving away from the receiver and negative in the reverse direction. -
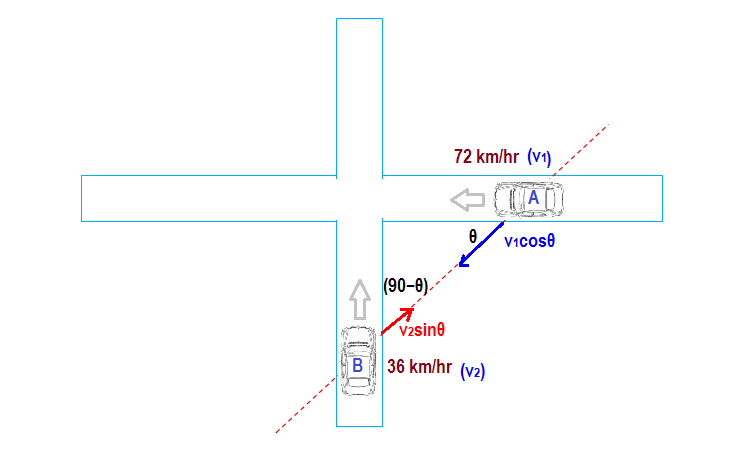
Let at an instant the line joining the position of 1st car (
#A# ) and position of the 2nd car (#B# ) makes an angle#theta# with the direction of motion of the first car. So this line will make angle#(90-theta)^@# with the direction of motion of the 2nd car. -
So the component of velocity of the 1st car along
#AB# will be#v_(AB)=v_1costheta# ,where#v_1# is the velocity of the 1st car towards the crossing. -
And the component of velocity of the 2nd car along
#BA# will be#v_(BA)=vcos(90-theta)=v_2sintheta# , where#v_2# is the velocity of the 2nd car towards the crossing.
So
#v_r=v_2sintheta#
and
Now the equation [1] becomes
#nu= ((v+v_2sintheta)/(v-v_1costheta))nu_0#
Now
-
#v_1=72km"/"hr=20m"/"s# -
#v_2=36km"/"hr=10m"/"s# -
#v==340m"/"s# -
#nu_0=280Hz#
So
#nu= ((340+10sintheta)/(340-20costheta))280# Hz
When
#nu= ((340+10sin45)/(340-20cos45))280~~298# Hz

