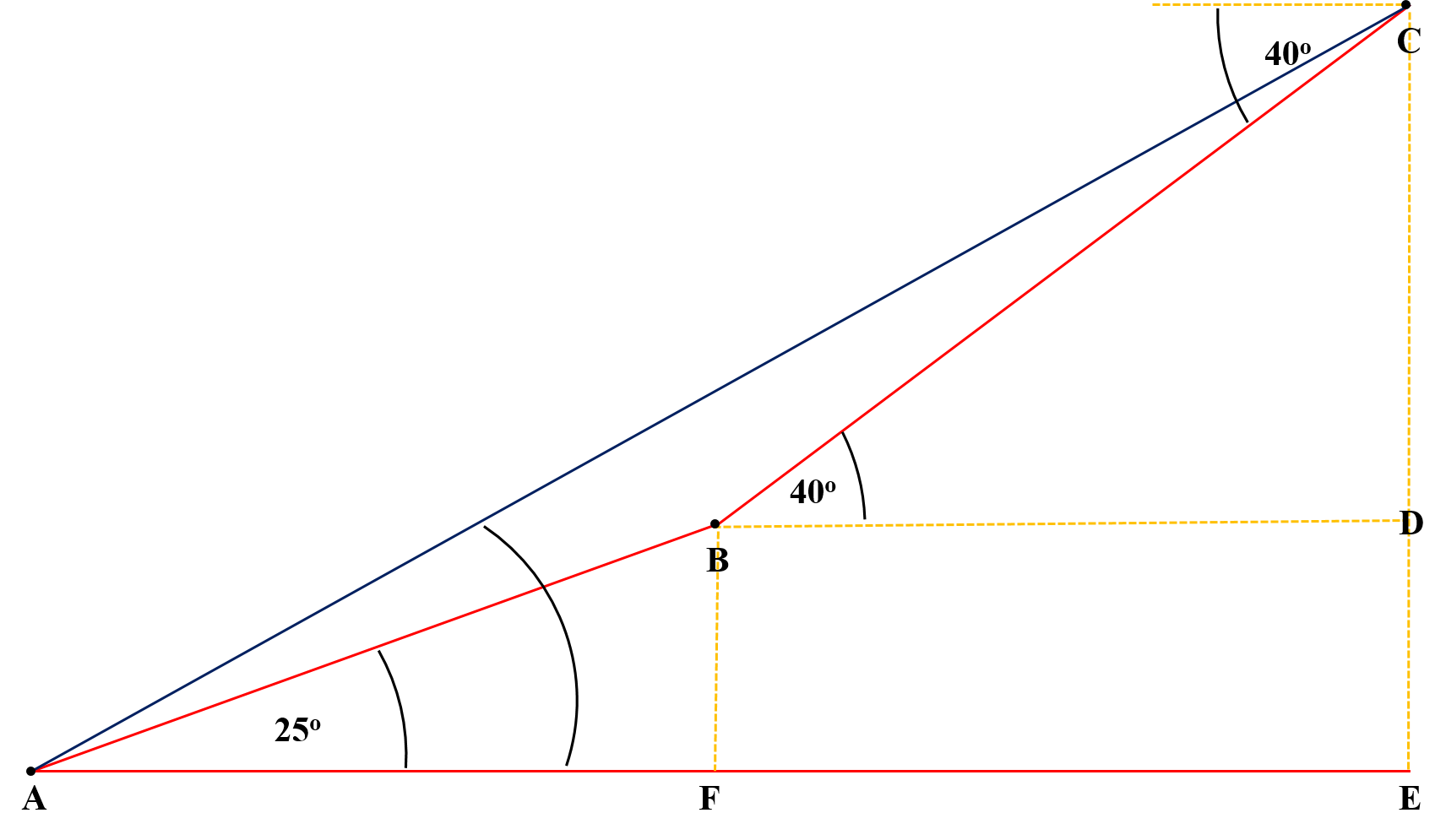
We can construct this diagram from the given information.
Let length of #AB# be #l_1# and length of #BC# be #l_2#.
It is given that #l_1/l_2 = 2/3# #-># 1.
Also, observe that #BD = FE# and #BF=DE#. #-># 2.
We have to find #angle CAE# which will give us elevation of C from A.
Let #angle CAE# be #theta#.
From #triangle ABF# we observe that:-
#[BF]/ [AB] = sin 25^o => BF = AB*sin 25^o = 0.423*l_1#
#therefore# using 2., #DE=0.423*l_1# #-># 3.
#[AF]/[AB] = cos 25^o => AF = AB*cos25^o = 0.906*l_1# #-># 4.
From #triangle BCD# we find:-
#[CD]/[BC] = sin40^o => CD = BC*sin40^o = 0.643*l_2# #-># 5.
#[BD]/[BC] = cos40^0 => BD = BC*cos40^o = 0.766*l_2#
#therefore# form 2., #FE=0.766*l_2# #-># 6.
Now,
#tan theta = [CE]/[AE] = [CD+DE]/[AF+FE]#
Substituting values of #DE, AF, CD, FE# from 3., 4., 5., 6.
#tan theta = [0.643*l_2 + 0.423*l_1]/[0.766*l_2 + 0.906*l_1]#
Dividing the numerator and deniminator by #l_2#
#=> tan theta = [0.643*cancel(l_2/l_2) + 0.423*l_1/l_2]/[0.766*cancel(l_2/l_2) + 0.906*l_1/l_2]#
Substituting value of #l_1/l_2# from 1.
#=> tan theta = [0.643 + 0.423*2/3]/[0.766+0.906*2/3] = 0.675#
#therefore theta = tan^-1 0.675 approx 34^o#
#therefore color(red)[angleCAE = 34^o] # which is the angle of elevation of #C# from #A#.




