How do we rationalize ionization energies?
1 Answer
You speak of ionization potentials:.........
Explanation:
And given the definition of ionization energy:
From purely electrostatic grounds, would we would not expect that
But these ionization energies ALSO reflect the electronic structure of the atom. Successive ionization enthalpies may require the removal of an electron from a non-valence shell, and thus the energy should be disproportionately high. The third ionization energy of magnesium, (say), requires the removal of an INNER, non-valence shell electron.
As chemists, as physical scientists, we should examine the data.
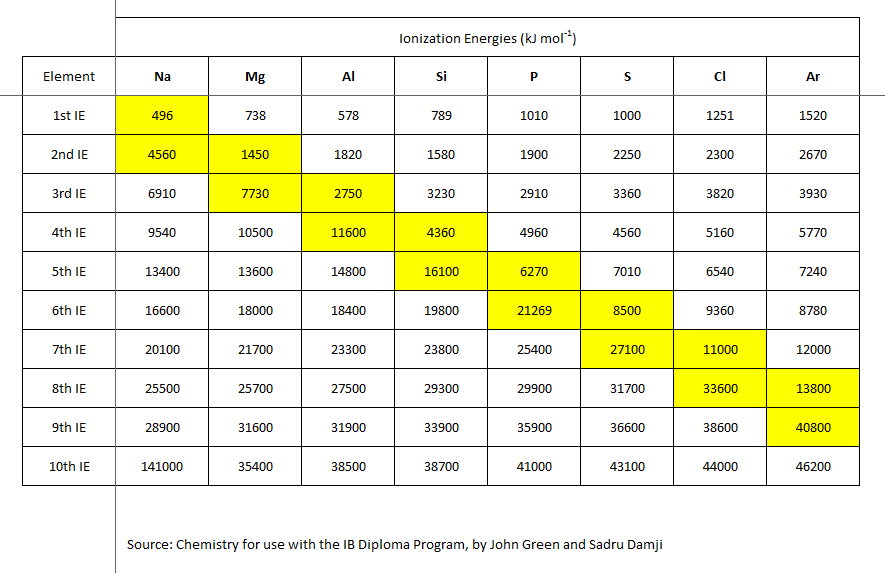
Why is the second ionization energy of sodium metal so disproportionately high? Why is the third ionization energy of magnesium metal so disproportionately high? And the yellow hatchings fairly dramatically represent the EXTRA energy required for ionization of an inner shell, non-valence electron. Of course, our understanding and conceptualization of electronic structure draws from these data.

