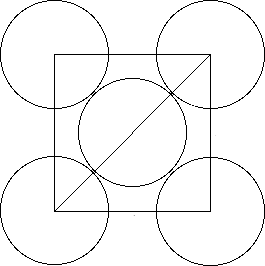Question #ee4f4
1 Answer
Explanation:
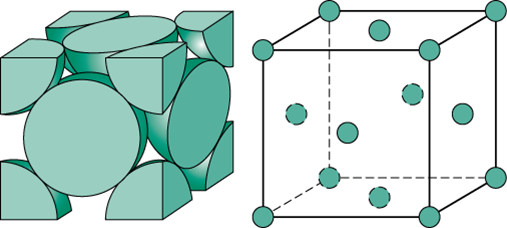
The idea here is that you need to use the configuration of a face-centered cubic unit cell to find a relationship between the length of the cell, which is usually labeled
So, a face-centered cubic unit cell looks like this
Now, you should know that the diagonal of a square is equal to
#"diagonal" = "side" xx sqrt(2)#
In this case, the diagonal of a face has a length of
#"diagonal" = r + 2r + r = 4r#
Here
This means that the length of the side of the unit cell
#"side" = "diagonal"/sqrt(2)#
will be equal to
#a = (4r)/sqrt(2) = (4r sqrt(2))/2 = 2sqrt(2) * r#
Plug in your value to find
#a = 2 sqrt(2) * "0.144 nm" = color(darkgreen)(ul(color(black)("0.407 nm")))#
The answer is rounded to three sig figs.