Question

Explain the forces acting, including friction, when an object is stationary or moving on an inclined plane. What coordinate system do we use?

Answer 1

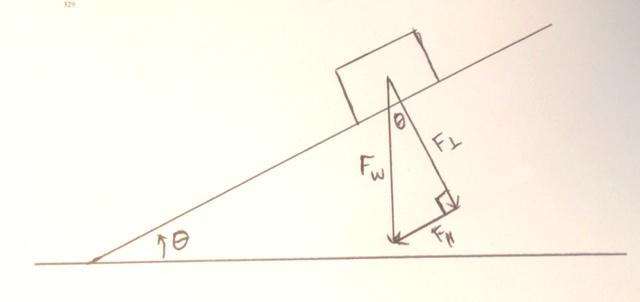
Three forces act:

`F_"//" = F_w sin \theta = mg sin \theta`

`F_"|--" = F_w cos \theta = mg cos \theta`

`F_"frict" = \mu F_"|--"`

Explanation:

The forces acting are a normal force at right angles to the plane, an accelerating force parallel to the plane and 'downhill', and a frictional force parallel to the plane and 'uphill'. The fundamental cause of all these forces is the weight force on the object, acting directly downward toward the centre of the earth.

The gravitational force is the key to the whole situation. It is given by `F_w=mg` where `g=9.8` or `10` `Nkg^-1` (the unit used is often `ms^-2`, which is equivalent to `Nkg^-1`, but I find the latter unit more direct and explanatory).

Using the image above, note that the slope is at an angle `\theta` to the ground, and that, by similar triangles, the angle between the weight force `F_w` and the normal force, `F_"|--"`, is also `\theta`.

The constructed triangle is a right-angled triangle, so we can use trigonometry. `F_w` is the hypotenuse, `F_"|--"` is the adjacent side (to the angle `\theta` and `F_"//"` is the opposite side.

Using the definitions `sin \theta = (opp)/(hyp)` and `cos \theta = (adj)/(hyp)`, and rearranging, gives:

`F_"//" = F_w sin \theta = mg sin \theta`

`F_"|--" = F_w cos \theta = mg cos \theta`

Finally, the frictional force will act in the opposite direction to `F_"//"` and will have a magnitude given by `F_"frict" = \mu F_"|--" =\mumgcos\theta`, where `mu` is the friction coefficient.

Answer 2

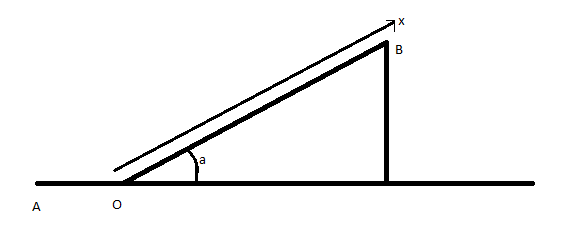
By rotating the axes to be aligned with the plane.

Explanation:

You take the axes and align them with the plane, so that the coordinates are 'parallel to the plane and perpendicular to the plane', rather than 'horizontal and vertical':

You draw the forces involved:

If your object is not moving use Newton's first law:
`sumF=0`
If your object is moving use Newton's second law:
`F=ma`