Question #611c6

Question

1584 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-05-27T17:03:31

The answer is #-1.1832#.

Follow the image, please.

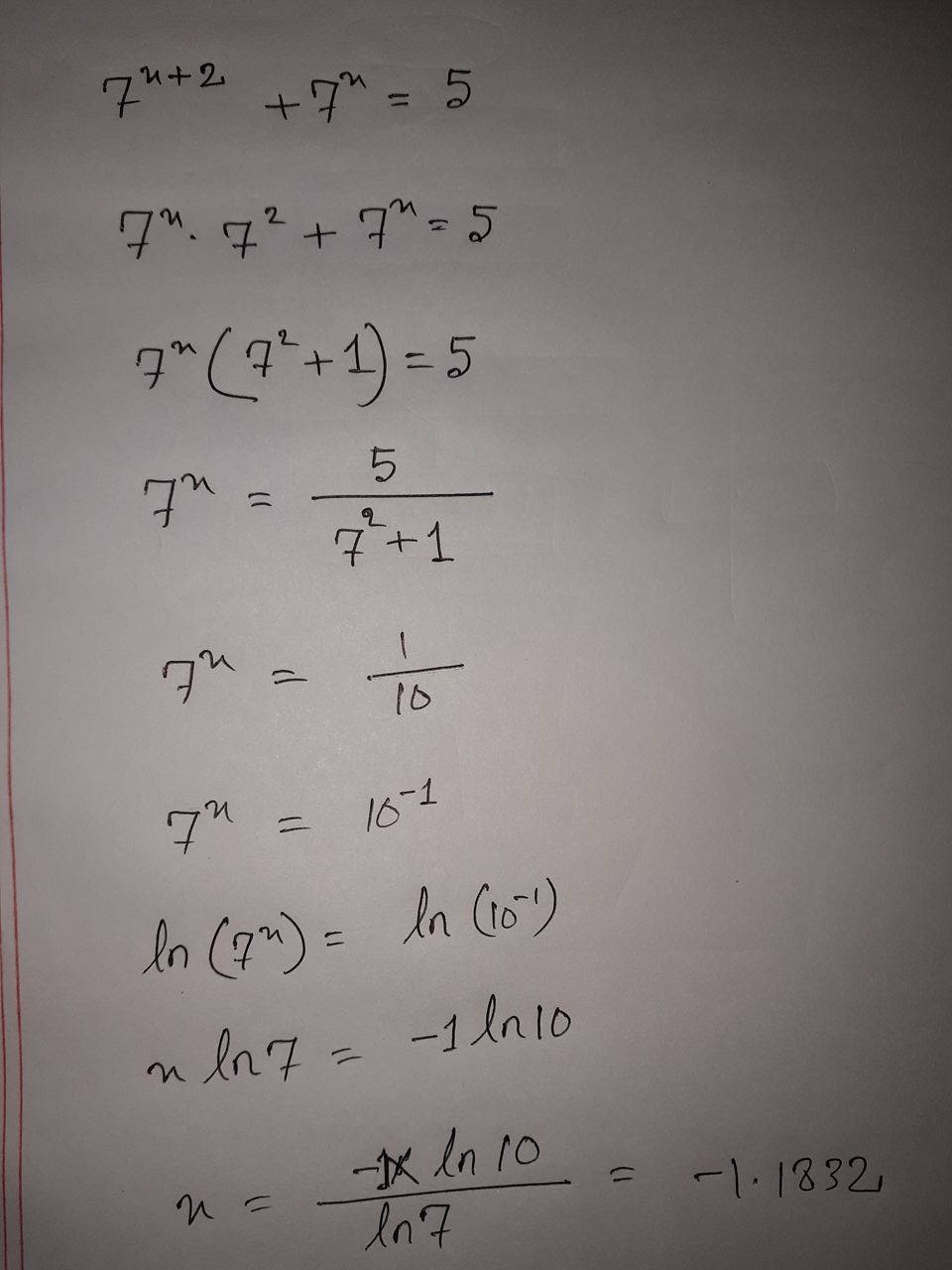
enter image source here

Answer 2 · 2017-05-27T17:06:22

Given: #7^(x+2) + 7^x=5#

Use the property that says addition of exponents is the same as multiplication of the base to each respective exponent:

#7^2 7^x + 7^x=5#

There is a common factor of #7^x# that can be moved outside parentheses:

#(7^2 + 1)7^x=5#

Square 7:

#(49 + 1)7^x=5#

#(50)7^x=5#

Divide both sides by 50:

#7^x=5/50#

#7^x=1/10#

Use the base 10 logarithm on both sides:

#log_10(7^x)=log_10(1/10) = -1#

Use the property that brings the exponent outside of a logarithm:

#xlog_10(7)=-1#

#x = -1/log_10(7)#