Question #0616a
1 Answer
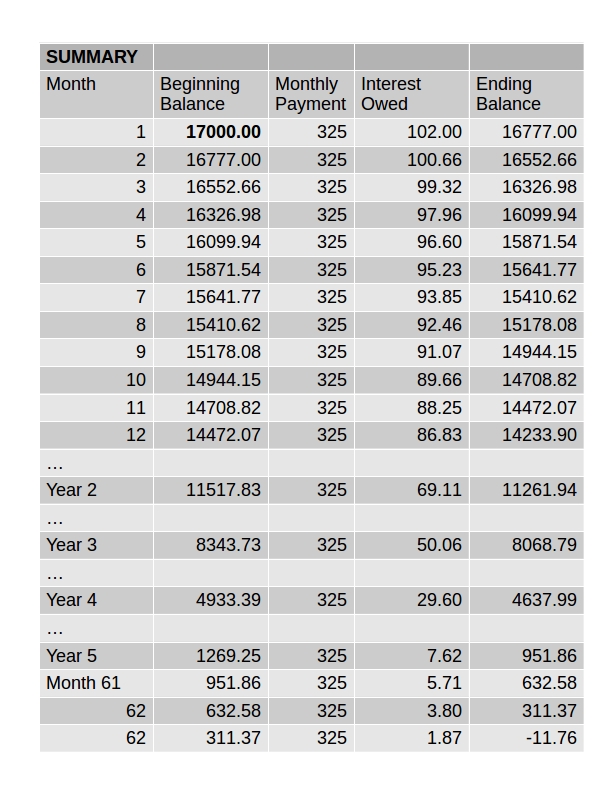
63 months
Explanation:
This is a very practical compound interest problem. It is a bit trickier than a straight accumulation problem because the amount on which the interest is calculated changes with every payment.
There is a direct formula for the calculation, but to understand how it works better and to use it for personal situations I prefer to calculate each step individually. I use a spreadsheet program to make the repetitive calculations easier. Then, given a principle amount, an interest rate and payment schedule, the pay-down can be calculated and the number of years or months for repayment determined.
The interest rate charged on the principle depends on the time period. An annual rate, compounded monthly, means that
The advantage of a spreadsheet program with individual entries instead of a straight time formula is that you can “play games” with the amounts to see how missed or late payments, or early/additional payments affect the payback period and the total interest paid. For this problem we have P = 17000, r = 0.072 , and n = 12.
An amount is decreased by a fixed amount over a set time interval, and the new amount becomes the basis for the next interval interest calculation. The formula for compound interest is:
Where P is the principal (initial amount), r is the rate of interest (as a decimal, not percentage) and n is the number of times the interest is calculated during the interval (t) intervals (years, months), and t is the number of years.
A monthly payment of