Question

How do you calculate the ionization energy of a hydrogen atom in its ground state?

Answer 1

`"1313 kJ mol"^(-1)`

Explanation:

!! VERY LONG ANSWER !!

Start by calculating the wavelength of the emission line that corresponds to an electron that undergoes a `n=1 -> n = oo` transition in a hydrogen atom.

This transition is part of the Lyman series and takes place in the ultraviolet part of the electromagnetic spectrum.

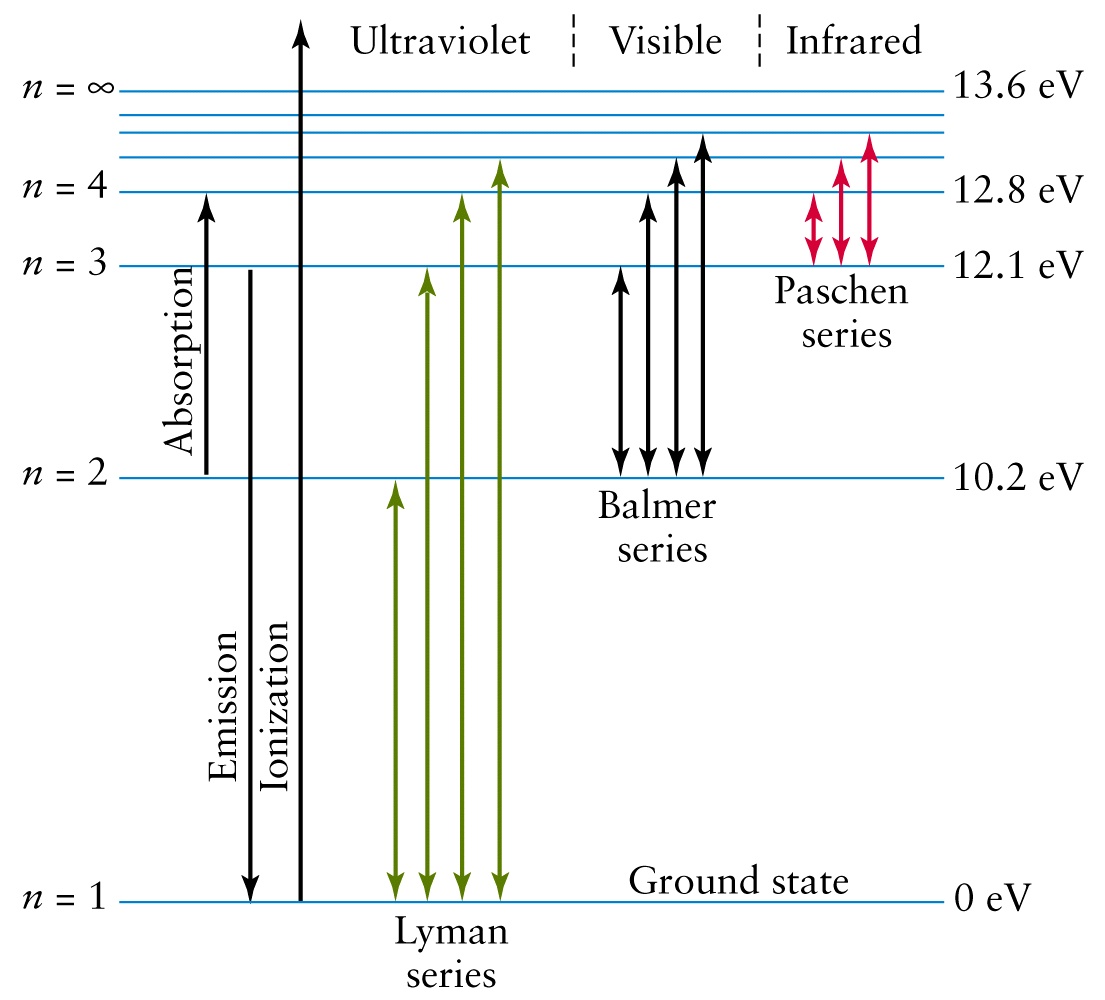http://www.physast.uga.edu/~rls/1010/ch5/ovhd.html

Your tool of choice here will be the Rydberg equation for the hydrogen atom, which looks like this

`1/(lamda_"e") = R * (1/n_1^2 - 1/n_2^2)`

Here

• `lamda_"e"` is the wavelength of the emitted photon (in a vacuum)
• `R` is the Rydberg constant, equal to `1.097 * 10^(7)` `"m"^(-1)`
• `n_1` represents the principal quantum number of the orbital that is lower in energy
• `n_2` represents the principal quantum number of the orbital that is higher in energy

In your case, you have

`{(n_1 = 1), (n_2 = oo) :}`

Now, you know that as the value of `n_2` increases, the value of `1/n_2^2` decreases. When `n=oo`, you can say that

`1/n_2^2 -> 0`

This implies that the Rydberg equation will take the form

`1/(lamda) = R * (1/n_1^2 - 0)`

`1/(lamda) = R * 1/n_1^2`

which, in your case, will get you

`1/(lamda) = R * 1/1^2`

`1/(lamda) = R`

Rearrange to solve for the wavelength

`lamda = 1/R`

Plug in the value you have for `R` to get

`lamda = 1/(1.097 * 10^(7)color(white)(.)"m") = 9.116 * 10^(-8)` `"m"`

Now, in order to find the energy that corresponds to this transition, calculate the frequency, `nu`, of a photon that is emitted when this transition takes place by using the fact that wavelength and frequency have an inverse relationship described by this equation

`color(blue)(ul(color(black)(nu * lamda = c)))`

Here

• `nu` is the frequency of the photon
• `c` is the speed of light in a vacuum, usually given as `3 * 10^8` `"m s"^(-1)`

Rearrange to solve for the frequency and plug in your value to find

`nu * lamda = c implies nu = c/(lamda)`

`nu = (3 * 10^(8) color(red)(cancel(color(black)("m"))) "s"^(-1))/(9.116 * 10^(-8)color(red)(cancel(color(black)("m")))) = 3.291 * 10^(15)` `"s"^(-1)`

Finally, the energy of this photon is directly proportional to its frequency as described by the Planck - Einstein relation

`color(blue)(ul(color(black)(E = h * nu)))`

Here

• `E` is the energy of the photon
• `h` is Planck's constant, equal to `6.626 * 10^(-34)"J s"`

Plug in your value to find

`E = 6.626 * 10^(-34)color(white)(.)"J" color(red)(cancel(color(black)("s"))) * 3.291 * 10^(15) color(red)(cancel(color(black)("s"^(-1))))`

`E = 2.181 * 10^(-18)` `"J"`

This means that in order to remove the electron from the ground state of a hydrogen atom in the gaseous state and create a hydrogen ion, you need to supply `2.181 * 10^(-18)` `"J"` of energy.

This means that for `1` atom of hydrogen in the gaseous state, you have

`"H"_ ((g)) + 2.181 * 10^(-18)color(white)(.)"J" -> "H"_ ((g))^(+) + "e"^(-)`

Now, the ionization energy of hydrogen represents the energy required to remove `1` mole of electrons from `1` mole of hydrogen atoms in the gaseous state.

To convert the energy to kilojoules per mole, use the fact that `1` mole of photons contains `6.022 * 10^(23)` photons as given by Avogadro's constant.

You will end up with

`6.022 * 10^(23) color(red)(cancel(color(black)("photons")))/"1 mole photons" * (2.181 * 10^(-18)color(white)(.)color(red)(cancel(color(black)("J"))))/(1color(red)(cancel(color(black)("photon")))) * "1 kJ"/(10^3color(red)(cancel(color(black)("J"))))`

`= color(darkgreen)(ul(color(black)("1313 kJ mol"^(-1))))`

You can thus say that for `1` mole of hydrogen atoms in the gaseous state, you have

`"H"_ ((g)) + "1313 kJ" -> "H"_((g))^(+) + "e"^(-)`

The cited value for the ionization energy of hydrogen is actually `"1312 kJ mol"^(-1)`.

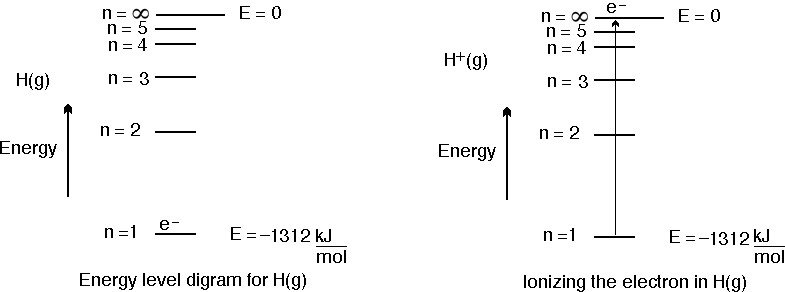http://genchem1.chem.okstate.edu/BDA/BCE22.php

My guess would be that the difference between the two results was caused by the value I used for Avogadro's constant and by rounding.

`6.02 * 10^(23) -> "1312 kJ mol"^(-1)" vs "6.022 * 10^(23) -> "1313 kJ mol"^(-1)`