Question

Question #9fbfb

Answer 1

`6.0 * 10^(22)` `"atoms S"`

Explanation:

The trick here is to realize that sulfur exists as an octatomic molecule under standard conditions.

In other words, sulfur exists as molecules that contain `8` atoms of sulfur. The chemical formula for octatomic sulfur is `"S"_8`.

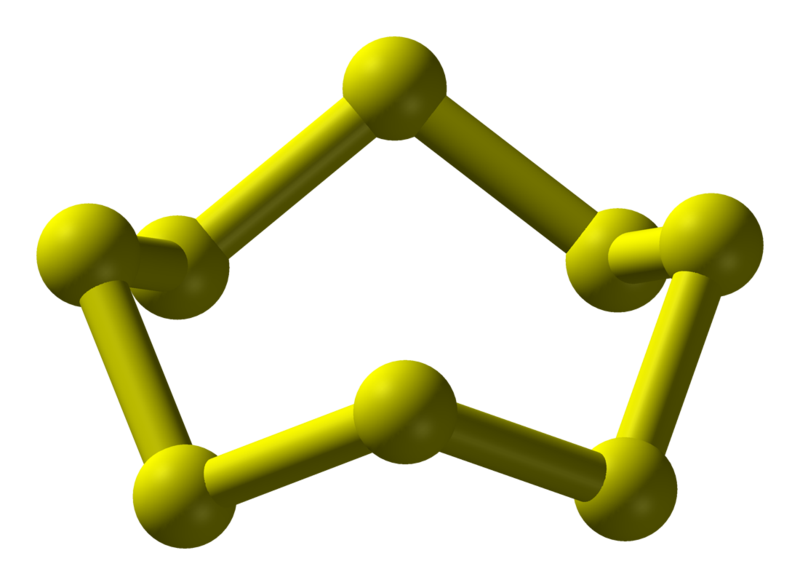
This implies that `1` mole of sulfur molecules will be equivalent to `8` moles of sulfur atoms. Consequently, the molar mass of octatomic sulfur will be equal to

`8 * overbrace("32.065 g mol"^(-1))^(color(blue)("the molar mass of elemental sulfur")) = "256.52 g mol"^(-1)`

You can thus say that `"3.2 g"` of sulfur will contain

`3.2 color(red)(cancel(color(black)("g"))) * "1 mole S"_8/(256.52color(red)(cancel(color(black)("g")))) = "0.012475 moles S"_8`

The number of octatomic sulfur molecules present in this sample will be equal to

`0.012475 color(red)(cancel(color(black)("moles S"_8))) * overbrace((6.022 * 10^(23)color(white)(.)"molecules S"_8)/(1color(red)(cancel(color(black)("mole S"_8)))))^(color(blue)("Avogadro's constant")) = 7.51 * 10^(21)` `"molecules S"_8`

Since each molecule of octatomic sulfur contains `8` atoms of sulfur, you can say that your sample contains

`7.51 * 10^(21) color(red)(cancel(color(black)("molecules S"_8))) * "8 atoms S"/(1color(red)(cancel(color(black)("molecule S"_8)))) = color(darkgreen)(ul(color(black)(6.0 * 10^(22)color(white)(.)"atoms S")))`

The answer is rounded to two sig figs, the number of sig figs you have for the mass of the sample.