This is a related rates problem. For problems like this, it's key to draw a picture. Consider the diagram below:
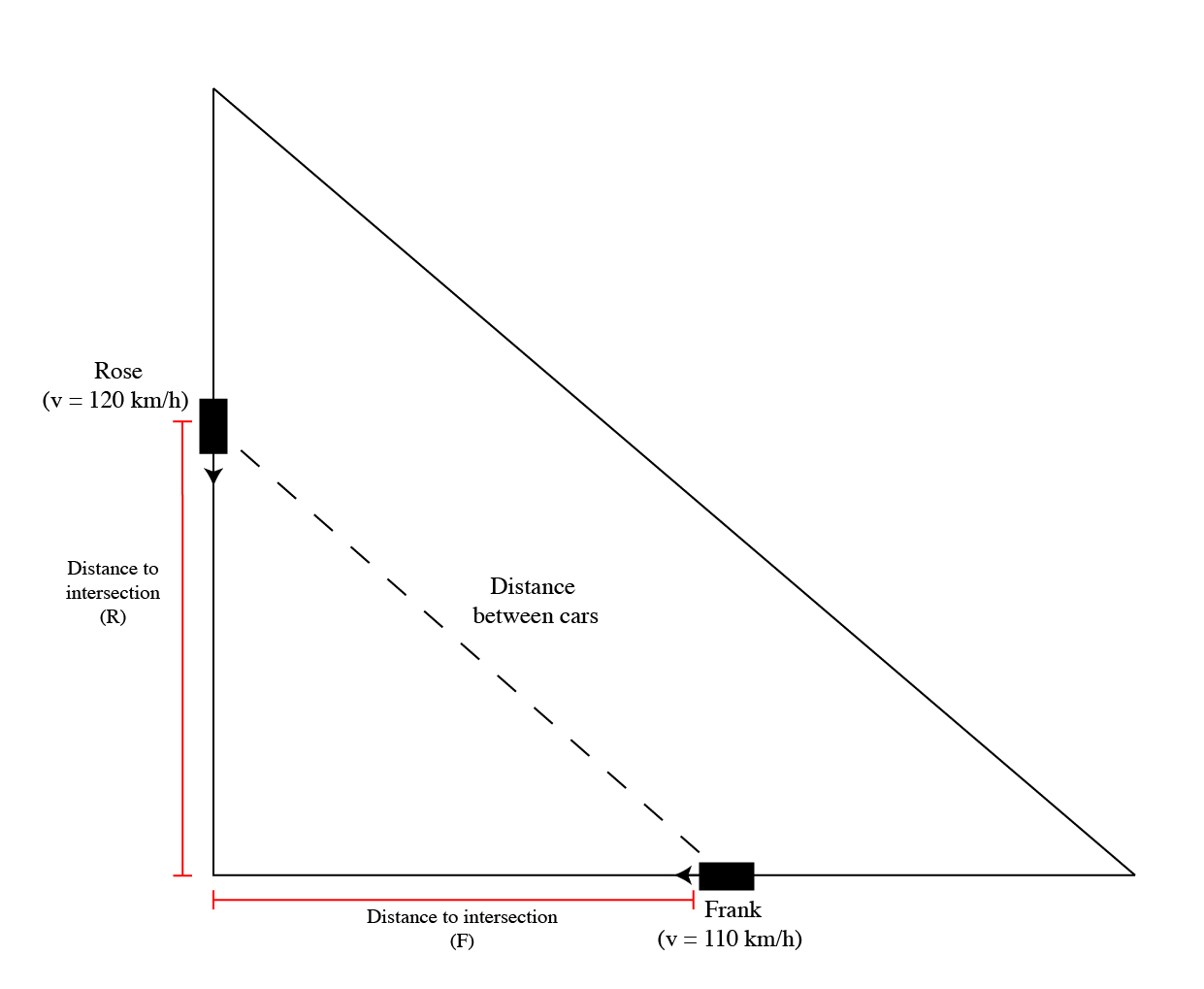
Next, we write an equation. If we call #R# the distance between Rose's car and the intersection, and #F# the distance between Frank's car and the intersection, how can we write an equation finding the distance between the two at any given time?
Well, if we use pythogorean theorum, we find that the distance between the cars (call that #x#) is:
#x = sqrt(F^2 + R^2)#
Now, we need to find the instantaneous rate of change #x# with respect to time (#t#). So, we take the derivative of both sides of this equation with respect to time. Note that you'll need to use implicit differentiation:
#xdx/dt = 1/2(F^2 + R^2)^(-1/2)* [2F(dF)/dt + 2R(dR)/dt]#
I skipped over the differentiation process for sake of time, but you'd need to use a chain rule to work with the square root, and implicit differentiation everywhere else.
Now, we plug in what we know. Note that the speeds provided in the diagram are rates of change of R and F, while we are given that #R = 0.5# and #F = 0.6# at a given instant of time. Plugging this in:
#xdx/dt = 1/2((0.6)^2 + (0.5)^2)^(-1/2)* [2(0.6)(-110) + 2(0.5)(-120)]#
Note: Speeds are negative since technically, the values of F and R (distances to intersection) are decreasing with time.
What about #x#? Well, let's go back to our starting equation:
#x = sqrt(F^2 + R^2)#
We know #F# and #R#, so we just solve for #x#:
#x = sqrt(0.6^2 + 0.5^2) ~~ 0.781#
Now, we just solve for #dx/dt#:
#dx/dt = (1/2((0.6)^2 + (0.5)^2)^(-1/2)* [2(0.6)(-110) + 2(0.5)(-120)])/(0.781)#
#= -206.6 " km/h"#
What does this mean? Well, it means that the distance between the two cars is changing at a rate of #-206.6# km/h. Alternatively, you could say that the distance between the two cars is decreasing at a rate of #206.6# km/h. Be very careful with your wording. The question asks for the rate at which it's decreasing, so you would just input the positive value.
Hope that helped :)


