Question #45a2e
1 Answer
Explanation:
The thing to remember about a balanced chemical equation is that the stoichiometric coefficients that are added to each chemical species can be treated as moles.
In your case, you know that
color(blue)(2)"H"_ 2"O"_ ((l)) -> 2"H"_ (2(g)) + "O"_ (2(g))
Notice that it takes
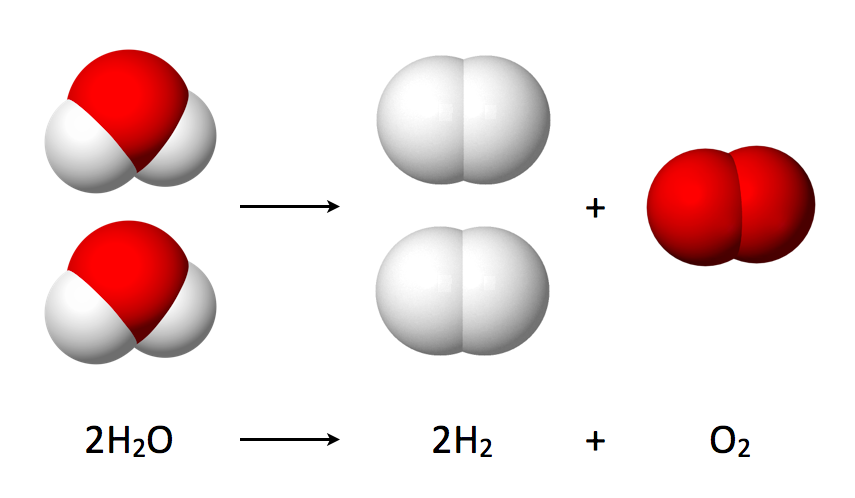 https://en.wikipedia.org/wiki/Water_splitting
https://en.wikipedia.org/wiki/Water_splitting
Since a mole is simply a very large collection of molecules, you can say that it takes
This is equivalent to saying that water and oxygen gas have a
This means that
6.2 color(red)(cancel(color(black)("moles H"_2"O"))) * "1 mole O"_2/(color(blue)(2)color(red)(cancel(color(black)("moles H"_2"O")))) = color(darkgreen)(ul(color(black)("3.1 moles O"_2)))
The answer is rounded to two sig figs, the number of sig figs you have for the number of moles of water.
So remember, the stoichiometric coefficients can be referred to as moles. The chemical formulas represent the reactants and the products that take part in the reaction.

