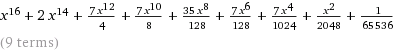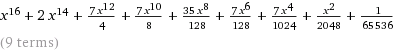#(x^2+2/8)^8#.
See Wikipedia for a formal explanation or MathIsFun for a more friendly one here. I'll show you how to figure this out using Pascal's triangle.
The term inside the brackets is called a binomial, since it has two terms. Let's consider the general binomial #(a+b)^n#. This always has an expansion of the form:
#(a+b)^n=C_0a^nb^0+C_1a^{n-1}b^1+...+C_{n-1}a^1b^{n-1}+C_na^0b^n#
While this looks fancy, just remember it as the exponent of #a# starting at #n# in the first term and going down to #0# in the last, and the exponent of #b# starting at #0# and going up to #n#. This means that expansion always has #n+1# terms. Thus, this expansion has 9 terms. Remember that #a^0# and #b^0# equal 1. We don't know what the coefficients #C_0,C_1,...,C_n# are yet.
Observing the pattern above, we observe that the fifth term has the form #Ca^4b^4#. So how do we find the coefficient? We use Pascal's triangle. Remember Pascal's triangle is formed so that each number in the next row is the sum of the two numbers above it:
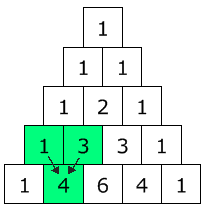
To find the coefficients, we find the row of the triangle with the same amount of numbers as terms, and those numbers correspond to the coefficients. If we continue Pascal's triangle, we get a row with 9 numbers:

We can see that the coefficients are: #1,8,28,56,70,56,28,8,1#. The fifth coefficient is #70#, thus the fifth term is #70a^4b^4#. In this case, #a=x^2# and #b=2/8=1/4#, so the fifth term is #35/128x^8#. For interest, the entire expansion is: