Question #aaeb4
3 Answers
Explanation:
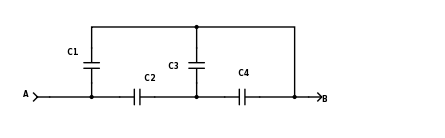
Given: Find the equivalent capacitance from A to B:
 www.digikey.com/schemeit/project
www.digikey.com/schemeit/project
Figure 1
Please observe that
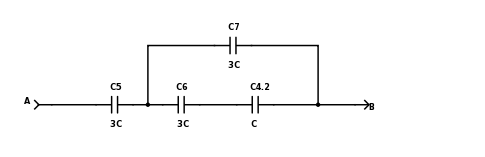
Figure 2 shows the Y network conversion of this:
 www.digikey.com/schemeit/project
www.digikey.com/schemeit/project
Figure 2
NOTE: Because my drawing tool does not allow me repeat component numbers between pages, I used C4.2 to represent the same capacitor C4 in figure 1. I will do this with other components as needed.
The calculations care taken from equation [5.7.1] of the reference :
Because they are all the same value,
Figure 2 is an easily solved series-parallel network.
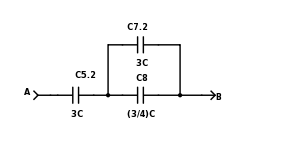
Figure 3 shows the combination of the 2 series capacitors:
 www.digikey.com/schemeit/project
www.digikey.com/schemeit/project
Figure 3
 www.digikey.com/schemeit/project
www.digikey.com/schemeit/project
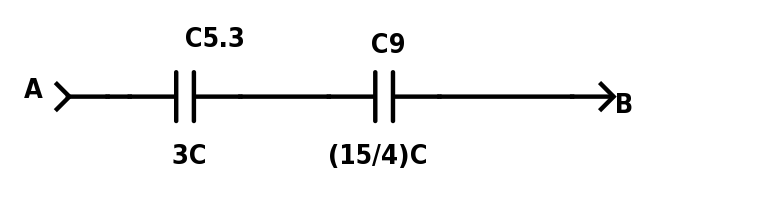
Figure 4
We are left with 2 capacitors in series:
The total equivalent capacitance is 1⅔ C (or 1.67 C to 3 s.f.).
Explanation:
The diagrams below show the rearrangement and simplification process step by step. There is a brief note or calculation that accompanies each step.
Starting layout . Nodes A and B shown, capacitance value of each capacitor is shown (C for all in this step).
I can redraw the layout of the junctions in the top right part of the circuit. I am not changing the essential layout of the circuit; just showing more clearly that the two capacitors on the right are in parallel.
Capacitors in parallel add up, so simplify the circuit by replacing the two in parallel with a single capacitor with capacitance 2C.
Redraw the circuit again to show more clearly the parallel and series arrangement.
The sum of the reciprocals of capacitors in series is equal to the reciprocal of the total equivalent capacitance:
So we simplify the series part of this circuit:
The last step is to simplify the remaining parallel arrangement. As above capacitors in parallel add up. So the total equivalent capacitance is 1⅔ C (or 1.67 C to 3 s.f.).
Yes, 5/3 C is correct. But .....
Explanation:
I have a different method being an Electronics Eng for 35 years.
.
Capacitors in series combine with the same formula as resistors in parallel ; 1/CT = 1/C1 + 1/C2 + 1/C3 + ....
However there is another method not taught in the textbooks.
It is called the N+ 1 Method .... for series C's OR parallel R's
It works for 2 C's or 2 R's at a time.
Method
1 / Take the ratio of two C's in question; call this 'n'
2 / Then just divide the larger C by 'n+1'
For example; 4C and C , n= 4 thus C[Total] = 4C/5
OR C and C , n=1 so C[Total] = C/2
This method works even when 'n' is a fraction and not an integer !!
For this problem we have 2 C's in parallel which are in series with another C and then the total in parallel with the last C
So
C + C = 2C
2C series C = 2C/3
2C/3 + C = 5C/3
:-))


