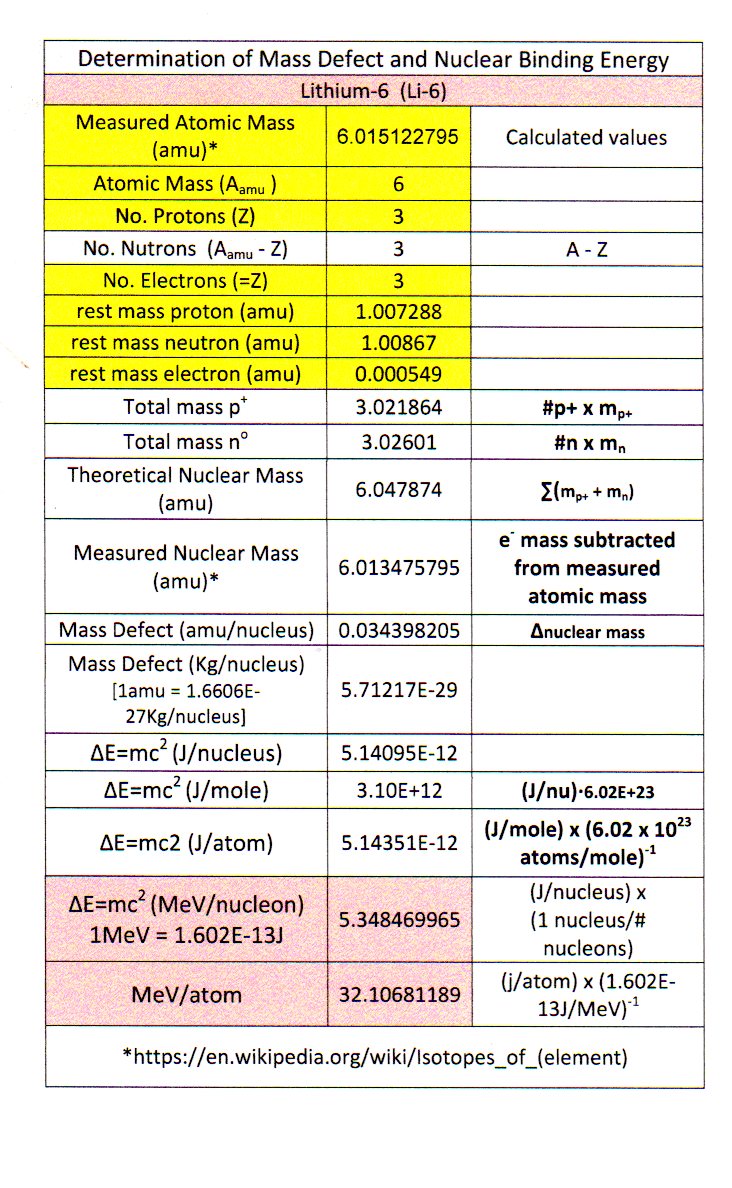
How do you determine the binding energy of lithium-6?
#m_p = "1.00728 amu"#
#m_n = "1.00867 amu"#
#m_e = "0.000549 amu"#
2 Answers
I got
And just to check, this graph shows the binding energy of
If we wanted, we could get
#"32.03 MeV"/"atom" xx "1 Li-6 atom"/"6 nucleons"#
#=# #"5.338 MeV/nucleon"#
which is fairly close to the
The binding energy is the energy that is needed to hold the nucleus together, and accounts for the small mass defect found in certain nuclides.
If we find the mass defect, i.e. how much less mass the nuclide has compared to the expected mass of the protons + neutrons, then it turns out that mass incorporated into
CALCULATING MASS DEFECT
The mass defect is given by
#M_d = (m_p + m_n) - (m_"exact" - m_e)# ,where:
#M_d# is the mass defect in#"amu"# .#m_p# is the rest mass of a proton in#"amu"# .#m_n# is the rest mass of a neutron in#"amu"# .#m_"exact"# is the exact nuclide mass in#"amu"# (including the electron(s)).#m_e# is the rest mass of an electron in#"amu"# .
Now, by recalling that the number of neutrons + protons is given by the mass number, and the number of protons by the atomic number, we have that
#M_d = [overbrace(3)^(Z) xx overbrace("1.00728 amu")^"Mass of one proton" + (overbrace(6)^(A) - overbrace(3)^(Z)) xx overbrace("1.00867 amu")^"Mass of one neutron"] - ("6.01512 amu" - 3 xx overbrace("0.000549 amu")^"Mass of one electron")#
#=# #"0.03438 amu"#
Now, what we'll need to do to get this to work with the Einstein relationship is to convert the mass to
I don't really remember how many
So, we have the per-atom mass defect as:
#M_d -= m = 0.03438 cancel"amu" xx (1/(6.0221413 xx 10^(23)) cancel"g" xx "1 kg"/(1000 cancel"g"))/cancel"amu"#
#= 5.708 xx 10^(-29)# #"kg/atom"#
CALCULATING BINDING ENERGY FROM MASS DEFECT
And so, the binding energy is given by:
#E = mc^2#
#= 5.708 xx 10^(-29)# #"kg"/"atom" xx (2.998 xx 10^(8) "m/s")^2#
#= 5.131 xx 10^(-12)# #"J/atom"#
And finally, in
#color(blue)(E) = (5.131 xx 10^(-12) cancel"J")/"atom" xx (cancel"1 eV")/(1.602 xx 10^(-19) cancel"J") xx "1 MeV"/(10^6 cancel"eV")#
#=# #color(blue)("32.03 MeV/atom")#
Li-6
MeV/atom 32.10681189
MeV/nucleon 5.348469965
Explanation:
Binding Energy of Li-6