Question

Question #6f780

Answer 1

`"please have a look at the fallowing details. (option c)"`

Explanation:

1- In order to understand the solution, we need to remember the following important points.

• An electric field is formed around the electric charges.
• Electric field is a vectorial quantity.
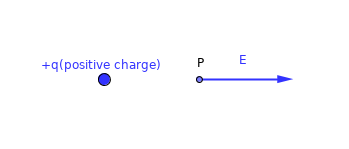
• The direction of the electric field generated by the electric charge with positive sign is directed outward from the charge.

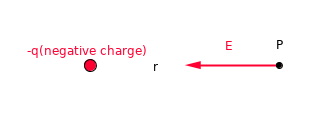
• The direction of the electric field generated by the electric charge in the negative sign is directed from the outside to the charge.

• We calculate the electric field intensity at a point far from an electric charge by using the following formula...

`E=k*q/r^2`

• The growth of r (away from load) causes the intensity of the electric field to decrease.

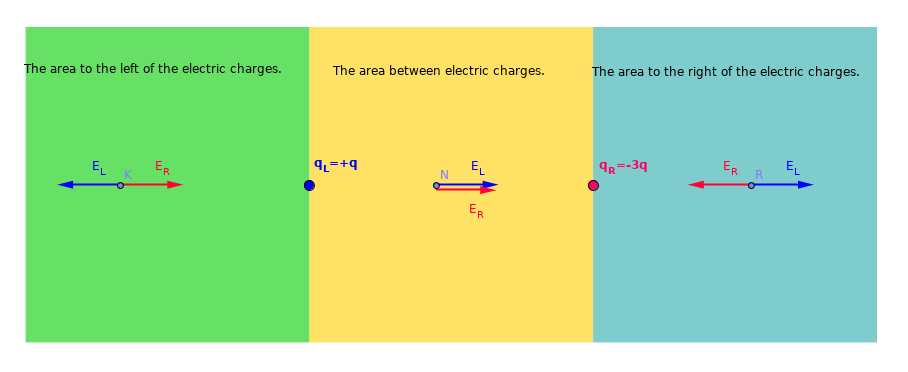
• In the given diagram space is colored by dividing into three regions.

• Two vectors representing the electric field in each region are drawn.
• Note the directions of the vectors in the regions.

• The point we are looking for can not be in the yellow zone (because the vectors are in the same direction).

• In order for the electric field to be zero, the magnitudes of the vectors must be equal and opposite.

• Which of the green or blue regions may be zero? we need to answer the question.

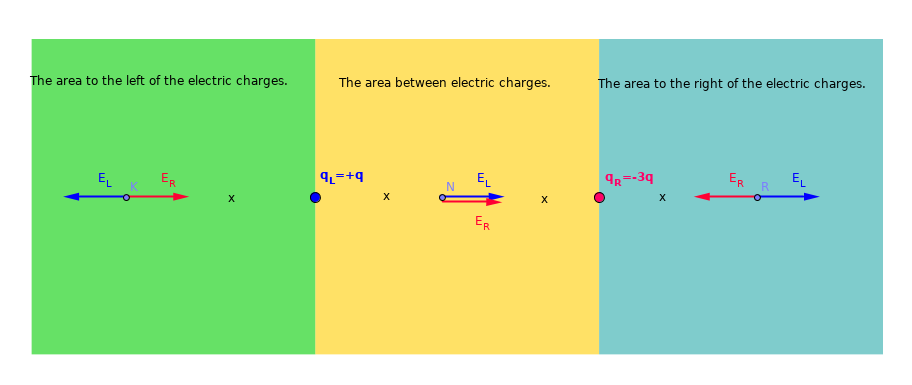
• To make it easier to understand, let's take the distance between points equally (indicated by x).

1. Now we can solve the problem.

2. Let's calculate the electric field at point K.

`vec E_K=k*(+q)/x^2+k*(-3q)/(2x)^2=(kq)/x^2-(3kq)/(4x^2)`

• Let's calculate the electric field at point R.

`vec E_R=k*(+q)/(4x)^2+k*(-3q)/(x)^2=(k q)/(16x^2)-(3kq)/x^2`

• Electric field intensity is proportional to the magnitude of the load and is inversely proportional to the distance.

`(3kq)/x^2>(k q)/(16x^2)`

• The point we're looking for is not in the blue zone.

• The intensity of the electric field can be zero in the green-painted space zone.