Total time = 20 s ⇒ #t_1 + t_2 + t_3 = 20# s
Total distance travelled, #s = vbar t = 5 × 20 = 100# m
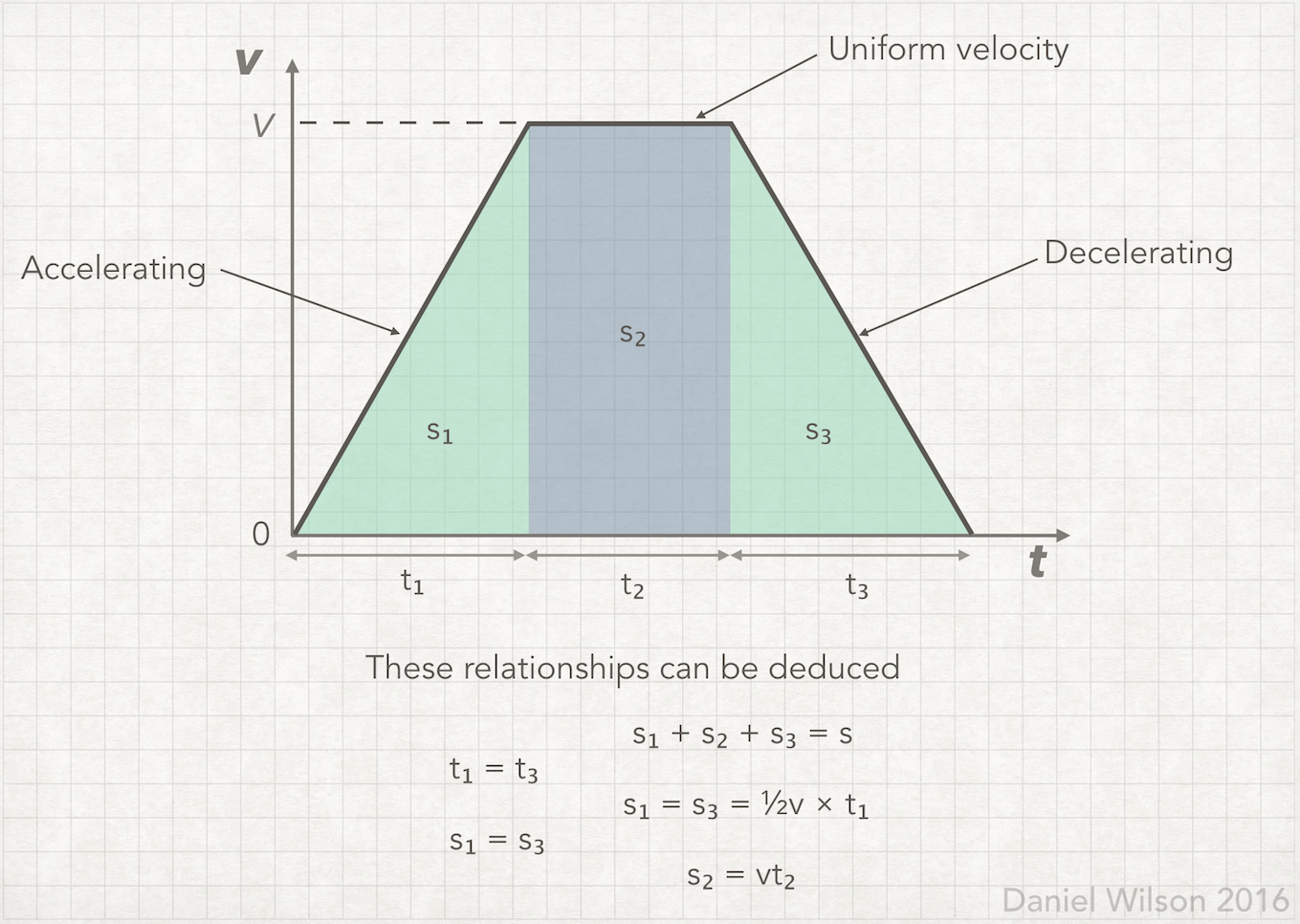
Acceleration for #t_1# equals deceleration at #t_3# and magnitude of velocity change is the same. For #t_1# change in velocity is #|v-0| = v# and for #t_3# change in velocity is #|0-v| = v#. So #t_1 = t_3#.
#∴ t_1 + t_2 + t_3 = 2t_1 + t_2 = 20# s ①
Average velocity for #t_1# and #t_3# is #v/2# as acceleration and deceleration are constant and final / initial velocity is zero.
Area under acceleration and deceleration lines:
#s_1 = v/2 × t_1#
#s_3 = s_1#
Total area under the graph:
#s = s_1 + s_2 + s_3 = 2s_1 + s_2 = s(v/2 × t_1) + vt = v(t_1 + t_2)#
#⇒ 100 = v(t_1 + t_2)# ②
Substitute for #t_2# in equation ② from equation ①:
① #⇒ t_2 = 20 - 2t_1#
② #⇒ 100 = v(t_1 + 20 - 2t_1)#
#⇒ 100 = v(20 - t_1)# ③
Use equation of constant acceleration for #t_1#;
#v = u + at ⇒ v = 0 + 2 × t_1 ⇒ v = 2t_1# ④
Substitute for #v# in ③ from ④:
③ #⇒ 100 = 2t_1(20 - t_1)#
#⇒ -2t_1^2 + 40t_1 - 100 = 0#
#⇒ t_1^2 - 20t_1 + 50 = 0#
Solutions for the quadratic equation:
#t_1 = (-b ± sqrt (b^2-4ac))/(2a)#
Variables of the formula: a = 1, b = -20, c = 50
#t_1 = (20 ± sqrt (400-4 × 1 × 50))/(2 × 1)#
#t_1 = (20 ± 14.14/2#
#⇒ t_1 = 2.93# s or #17.07# s
Use equation ① to solve for #t_2#:
Equation ① is : #2t_1 + t_2 = 20# s
#⇒ t_2 = 20 - 2t_1#
So #t_2# is either #14.14# s or #-14.14# s. Obviously it cannot be #-14.14# s! So the solution is that the vehicle drives at uniform velocity for #14.14# s.


