Estimate the area under the curve #f(x) = x^2# over the interval #[0,10]# with #5# strips using Left Riemann Sums?
2 Answers
Since you are using 5 sub intervals, your intervals would be divided like this:
The left riemann sum requires you to use the lower number in every interval listed above as your
Note that
Upon finding the individual areas of each of the five rectangles formed by the five sub-intervals evaluated at the "left side"
Alternatively, you could use the fact that all the rectangles are the same width, keeping
Therefore your left riemann sum would be
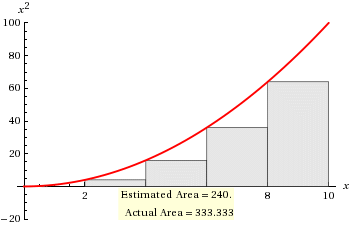
# LRS = 240 #
Explanation:
We have:
# f(x) = x^2 #
We want to calculate over the interval
# Deltax = (10-0)/5 = 2#
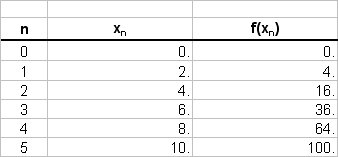
Note that we have a fixed interval (strictly speaking a Riemann sum can have a varying sized partition width). The values of the function are tabulated as follows;
Left Riemann Sum
# LRS = sum_(r=0)^4 f(x_i) \ Deltax_i #
# " " = 2 * (0 + 4 + 16 + 36 + 64) #
# " " = 2 * (120) #
# " " = 240 #
Actual Value
For comparison of accuracy:
# Area = int_0^10 \ x^2 \ dx #
# " " = [x^3/3]_0^10 #
# " " = 1/3[x^3]_0^10 #
# " " = 1/3(1000) #
# " " = 1000/3 #
# " " = 333.3333... #