Question #e4ab2
1 Answer
Explanation:
This looks like a job for the Clausius - Clapeyron equation, which looks like this
#color(blue)(ul(color(black)(ln(P_1/P_2) = (DeltaH_"vap")/R * (1/T_2 - 1/T_1))))#
Here
Now, you know that at an unknown atmospheric pressure
#T_2 = 110^@"C" + 273.15 = "383.15 K"#
Moreover, you know that at normal pressure, i.e. at
#T_1 = 100^@"C" + 273.15 = "373.15 K"#
As you know, a liquid boils when its vapor pressure is equal to the atmospheric pressure, so you can use the two atmospheric pressures in the Clausius - Clapeyron equation as
So, plug in your values into the equation to get
#ln("1 atm"/P_2) = ("40,660" color(red)(cancel(color(black)("J"))) color(red)(cancel(color(black)("mol"^(-1)))))/(8.3145 color(red)(cancel(color(black)("J"))) color(red)(cancel(color(black)("mol"^(-1)))) color(red)(cancel(color(black)("K"^(-1))))) * (1/(383.15 color(red)(cancel(color(black)("K")))) - 1/(273.15color(red)(cancel(color(black)("K")))))#
#ln("1 atm"/P_2) = -0.342041625#
This will be equivalent to
#e^ln("1 atm"/P_2) = e^(-0.342041625)#
which will get you
#"1 atm"/P_2 = 0.71032#
You can thus say that
#P_2 = "1 atm"/0.71032 = color(darkgreen)(ul(color(black)("1.4 atm")))#
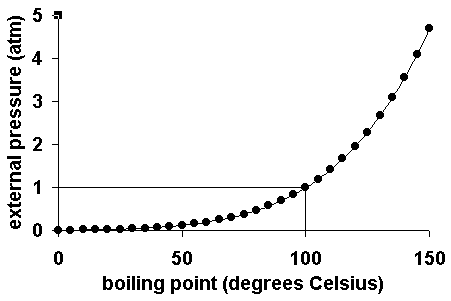
Now, does this result make sense?
As atmospheric pressure increases, the molecules of water will need more energy in order to escape from the liquid, which implies that the temperature of the water will be higher at the new boiling point.
So in your case, a higher boiling temperature implies a higher a higher value for the vapor pressure of water at its boiling point, i.e. a higher atmospheric pressure.