Question #b7819
1 Answer
Explanation:
For starters, you know that aluminium has an atomic number of
In order to become a
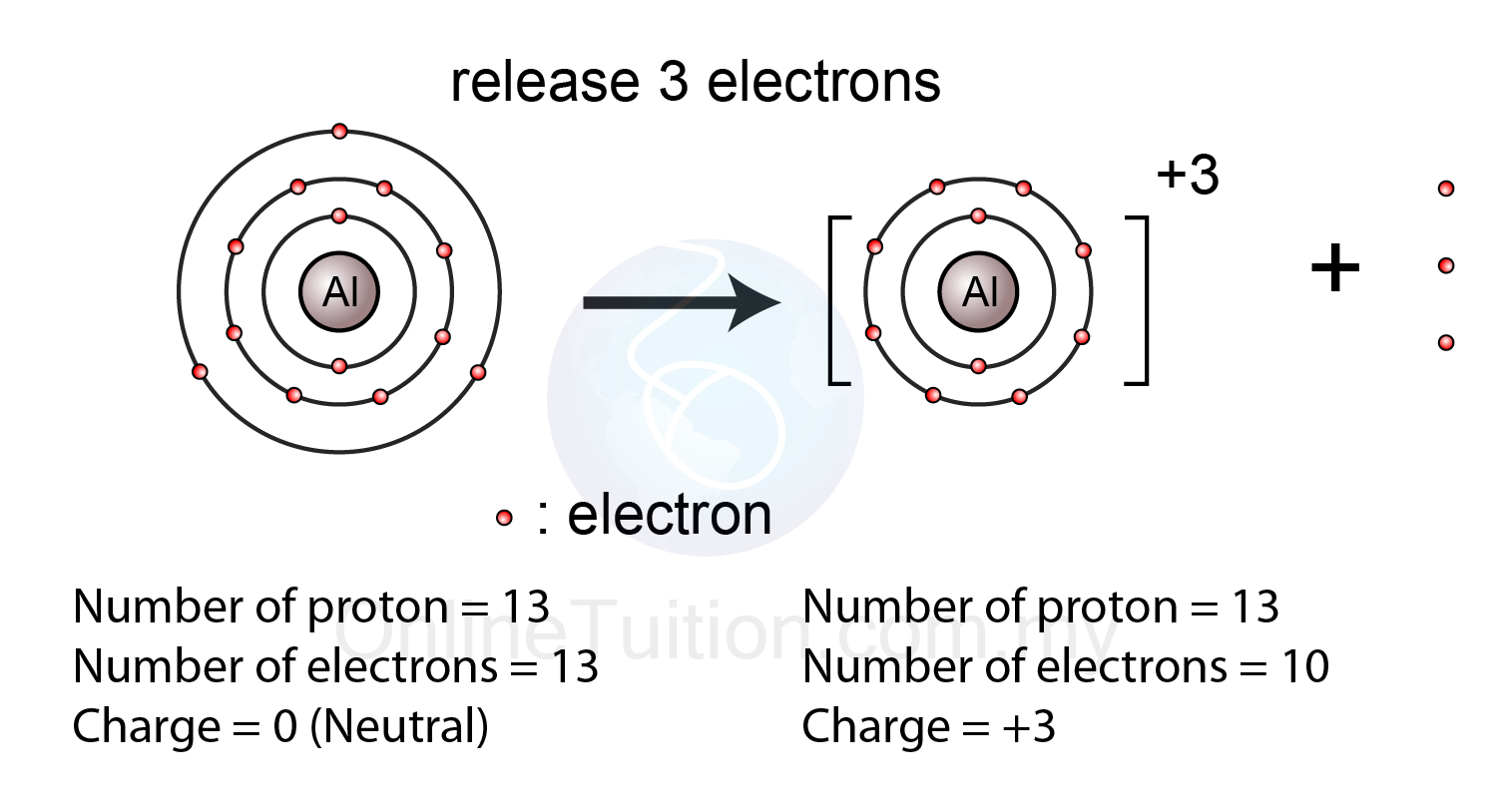
Now, you can safely assume that the mass of an aluminium cation is equal to the mass of a neutral atom of aluminium.
This implies that you can use the molar mass of aluminium to calculate the number of moles of aluminium cations present in your sample
#81 color(red)(cancel(color(black)("g"))) * "1 mole Al"^(3+)/(27.0color(red)(cancel(color(black)("g")))) = "3.0 moles Al"^(3+)#
As you know, in order to be able to say that you have
This means that your sample will contain
#3.0 color(red)(cancel(color(black)("moles Al"^(3+)))) * overbrace((6.022 * 10^(23)color(white)(.)"Al"^(3+)color(white)(.)"cations")/(1color(red)(cancel(color(black)("mole Al"^(3+))))))^(color(blue)("Avogaro's constant")) = 1.81 * 10^(24)# #"Al"^(3+)# #"cations"#
Finally, use the fact that every aluminium cation contains
#1.81 * 10^(24)color(red)(cancel(color(black)("Al"^(3+)"cations"))) * "10 e"^(-)/(1color(red)(cancel(color(black)("Al"^(3+)"cations")))) = color(darkgreen)(ul(color(black)(1.8 * 10^(25)color(white)(.)"e"^(-))))#
The answer is rounded to two sig figs, the number of sig figs you have for the mass of

