Question #9134c
1 Answer
Number of loops in the primary coil is
The primary current drawn from the line is
Both input and output power are the same at
Explanation:
To calculate numbers of loops and amps, it is important to understand how a transformer works. Its job is to receive electrical voltage and either reduce it to a smaller voltage for use in a house or to increase it to a higher voltage for transmission over long distances. The transformer does this by circling the voltage in loops of wire around an iron core to induce voltage in other loops of wire around the same core to result in a lower or higher voltage out.
Whenever the voltage is increased or decreased in a transformer, we must pay for the exchange in two ways. Some of the voltage is lost in the transformation, although transformers can be 98% efficient. The other payment comes in loss or gain of current, which is opposite that of the voltage.
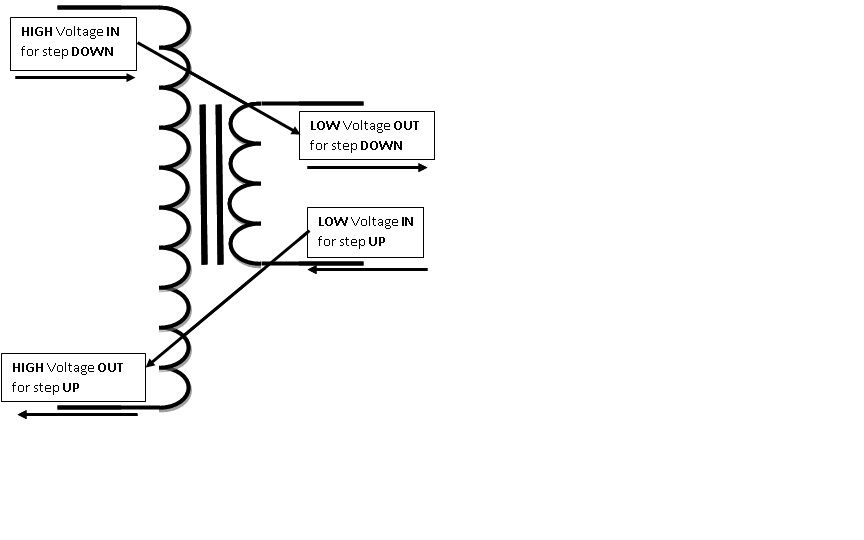
The reduction or increase in voltage is directly related to the number of loops of wire on either side of the core. More loops will be on the higher voltage side and less loops will be on the lower voltage side.
Now we can compare the primary and secondary voltages,
And we can compare the number of primary and secondary loops,
And as they are directly related:
Then, in this question:
When a transformer is used, [when voltage
Then we have:
To calculate the power input and output:
There is more information on transformer operation here:
http://jacobs-online.biz/understanding_transformers.htm
