Question

Question #fb988

Answer 1

Altitudes concur at orthocenter.
Meadians concur at centroid.

Explanation:

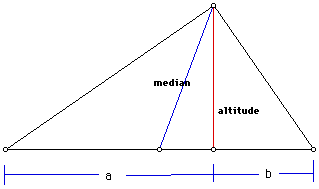
1. Altitude : Perpendicular line drawn from a vertex to the base of the triangle.
   Median : Line Dewan from a vertex to the midpoint of the base of a triangle.

2. Altitude may or may bisect the base (it divides the base equally in the case of isosceles and equilateral triangles).
   Median will bisect the base of the triangle always.

3. Altitude is always be perpendicular to the base.
   Median will be a perpendicular bisector to the base only in the case of an equilateral triangle; in the case of an isosceles triangle, only one median will be a perpendicular bisector and the other medians will not.

4. Meeting point of the three altitudes is the orthocenter. There is no specific distance of the orthocenter from the vertices.
   Meeting point of the three medians is the centroid. Centroid is two thirds of median length from the vertex and is one third from the corresponding base.

5. Orthocenter may or may not be within the triangle (will fall with in the triangle if the triangle is acute and outside if it is obtuse).
   Centroid is always within the triangle.