Question

Human proofreaders catch 70% of word errors. If a single essay contains 10 word errors, what is the distribution of the number of errors caught in this essay?

Answer 1

If `X` is the number of errors caught, then the intended answer is most likely `X" "~" ""Bin"(n=10, p=0.7).`

Explanation:

The wording of the question is a little confusing. There is a difference between "catching 70% of word errors" and "having a 70% chance of catching one error".

"Catching 70% of word errors" suggests a more accurate measure of the proofreaders' ability to catch errors, with minimal or no fluctuation in that 70% value. As such, it turns the question into a basic arithmetic problem, and the answer would be

`70% xx 10 " errors" = 7 " errors"`,

with (nearly) 100% probability.

If, on the other hand, we interpret the question to mean "Human proofreaders have a 70% chance of catching a word error", then each individual error has a 70% chance of being spotted. This is more in line with a proper probability distribution, because it's like tossing a coin that's weighted to have a 70% chance of landing on heads. If we toss the coin 10 times, the most probable outcome is indeed 7 heads, but there is certainly a chance of tossing heads anywhere from 0 to 10 times.

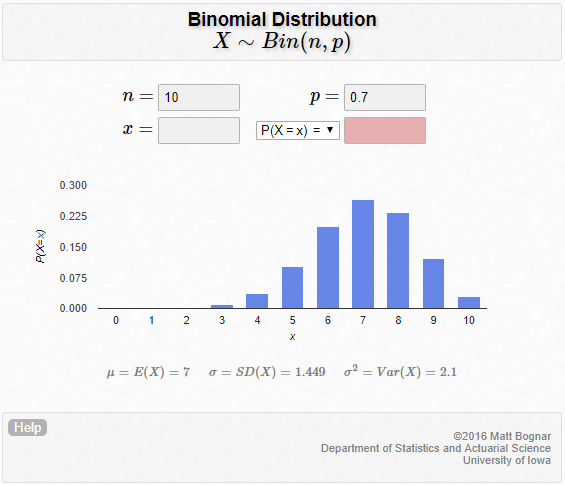
If we let `X` be the number of errors caught by our student proofreader, then the distribution for `X` is Binomial, with each of the `n=10` word errors having a `p=70%` chance of being caught. This is a discrete probability distribution, written as

`X" "~" Bin"(n=10, p=0.7)`,

or often just

`X" "~" Bin"(10, 0.7)`.

Here is a graph of the distribution: