There are some steps:
[Step1] Prove that #e^xcosx=1# has no negative root.
If #x<0#, the following must be satisfied:
#0< e^x <1#, #-1<= cosx <=1 #
#-> abs(e^xcosx)<1#
So, the roots #e^xcosx=1# must be 0 or greater.
[Step2] Find where the roots of #e^xcosx=1# lie.
Let #f(x)=e^xcosx-1#.
#f(0)=e^0*cos0-1=1*1-1=0# and #x=0# is the smallest root.
Differentiate #f(x)#:
#f'(x)=e^x(cosx-sinx)#
#=-sqrt(2)e^xsin(x-1/4pi)#
#x=(n+1/4)pi# satisfies #f'(x)=0# if #n>=0# is an integer.
Indeed, #f((2n+1/4)pi)# is a local maxima and #f((2n+5/4)pi)# is a local minima.
Here is a graph for #y=e^xcosx-1#.
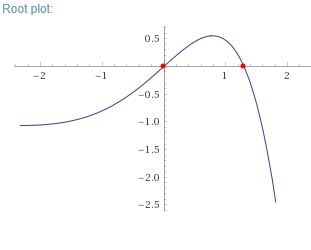
Let #x=alpha# is a positive root for #f(x)=0#.
#alpha# must satisfy #(2n+1/4)pi< alpha< (2n+1/2)pi# or #(2n+3/2)pi< alpha < (2n+2)pi# since:
#f((2n+1/4)pi)=e^((2n+1/4)pi)/sqrt(2)-1> 0# (Note that #e^(pi/4)=2.193...# is larger than #sqrt(2)#)
#f((2n+1/2)pi)=-1< 0#
#f((2n+3/2)pi)=-1<0#
#f((2n+2)pi)=e^((2n+2)pi)-1> 0#
There are no roots between #2npi< x<= (2n+1/4)pi# because f(x) is monotonically increasing in this range(#f'(x)> 0#).
Similarly, there are no roots between #(2n+1/2)pi<= x <=(2n+3/2)pi#. f(x) is always negative here.
So,
#color(red)("it is sufficient to prove that at least one root for " e^xsinx-1=0 " exists in the range " 2npi< x< (2n+1/4)pi or (2n+1/2)pi < x< (2n+3/2)pi.)#
[Step3] Prove the statement above(in red characters)
Let #g(x)=e^xsinx-1#.
#g(2npi)=-1< 0#
#g((2n+1/4)pi)=e^((2n+1/4)pi)/sqrt(2)-1> 0#
#g((2n+1/2)pi)=e^((2n+1/2)pi)-1> 0#
#g((2n+1)pi)=-1 <0#
The proof is completed via the intermediate value theorem.
Visualization:
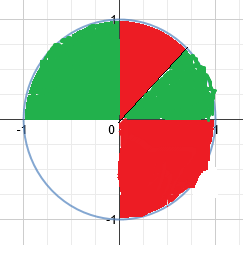
Roots for #e^xcosx-1=0# is in the red area and roots for #e^xsinx-1=0# is in the green area.



