Question

Question #31aef

Answer 1

`B~~9.6xx10^-3" T "`

Explanation:

Ampère's law gives the magnetic field (magnetic flux density) inside a solenoid as

`color(blue)(vecB=munIhatz)` (for a solenoid positioned vertically)

where:

• `mu` is the magnetic permeability constant
• `n` is the turn density `N//L`
• `I` is the current running through the solenoid

Note that the magnetic field outside of the solenoid is `0`. I will show the process for determining the field at the end, should that be useful.

We are given that `N//L=1270" turns"//"0.787m"` and `I=4.74"A"`. Additionally, we know that `mu_0=4pixx10^-7"T"//("A"*"m")` (assuming a vacuum). Then we have:

`B=4pixx10^(-7)*1270/0.787*4.74`

`=0.00961208" T"`

`=>color(blue)(B~~9.6xx10^-3" T ")`

`-------------------`

Magnetic field/flux density of a solenoid:

Consider a very long solenoid, consisting of `n` closely wound turns per unit length on a cylinder of radius `R`, each carrying a steady current `I`.

From the right hand rule, we expect that the magnetic field points upward inside the solenoid and downward outside.

Apply Ampère's law to two rectangular loops:

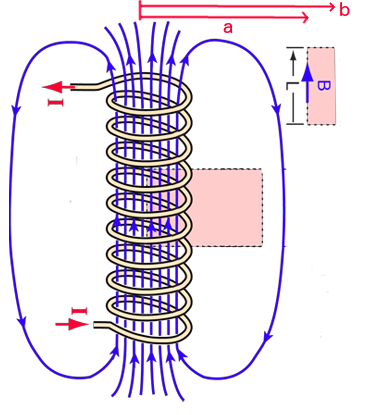
Loop 1 lies entirely outside the solenoid, with its sides at distances `a` and `b` from the axis:

`oint" "vecB*dvecl`

`=[B(a)-B(b)]L`

`=mu_0I_"enc"`

`=0`

Where `I_"enc"` is the current enclosed by the loop. For the loop outside of the solenoid there is no enclosed current, and hence `I_"enc"=0`.

Then is follows that `B(a)=B(b)`.

This indicates that the field outside of the solenoid does not depend on the distance from the axis. However, we know that the field must go to zero very far away from the solenoid. Therefore, it must be the case that the field is zero everywhere outside of the solenoid. Clever!

As for loop 2, which is half inside and half outside of the solenoid, Ampère's law gives:

`oint" "vecB*dvecl=BL`

`=mu_0I_"enc"`

`=mu_0nIL`

Hence, the magnetic field inside of a solenoid is given by `vecB=mu_0nILhatz`.