Question

How do you convert a fraction into a decimal?

Answer 1

Long divide the numerator by the denominator until the remainder repeats or you have as many digits as you want.

Explanation:

One way which is guaranteed to work is to long divide the numerator by the denominator.

Since the running remainder is a non-negative integer that is always less than the divisor, it will eventually repeat, at some time after you have exhausted the digits from the dividend.

So the decimal will always repeat or terminate (i.e. a repeating `0` remainder).

For example, to find the decimal representation of `1/7`, divide `1` by `7` ...

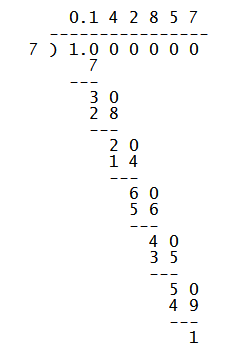
In this simple example, the remainder `1` recurs, so we can deduce that the digits `142857` will repeat from that point onwards and

`1/7 = 0.142857142857... = 0.bar(142857)`

Here's a much longer example to calculate the exact decimal representation of `114/268` ...

Notice that the remainder `68` repeats, so we find:

`114/268 = 0.4bar(253731343283582089552238805970149)`

In this particular case, we could have identified the common factor `2` of the numerator and denominator before we started the long division and instead divided `57` by `134`, but it would give the same result.

If the simplest form of the fraction has a denominator whose only prime factors are `2` and/or `5` then the long division will terminate, so the decimal representation will terminate.