Question #8ed74
1 Answer
Sep 17, 2017
Explanation:
To find the inverse,
However, since the domain of
So,
Any function and its inverse will be reflections of each other over the line
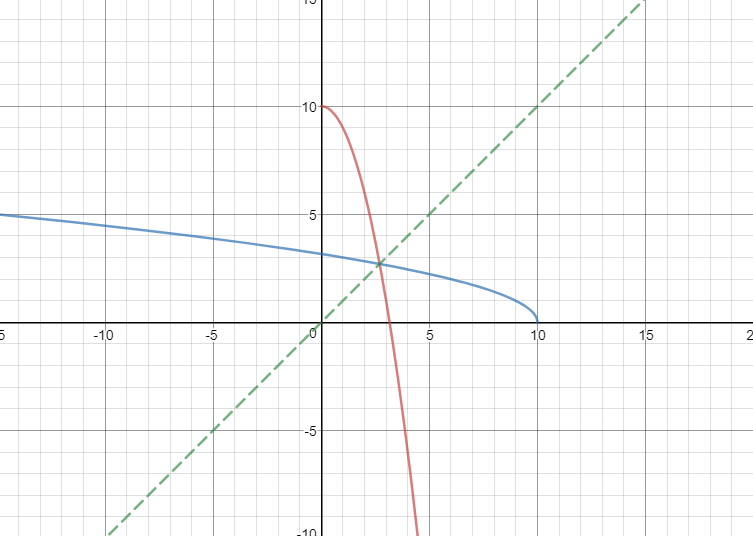
To find the inverse,
However, since the domain of
So,
Any function and its inverse will be reflections of each other over the line
