Question #bfd15
1 Answer
The work required to raise the anchor and chain is 22.3 kJ
Explanation:
Being that I am British I use the SI system. I have converted all values to SI equivalents to solve this problem.
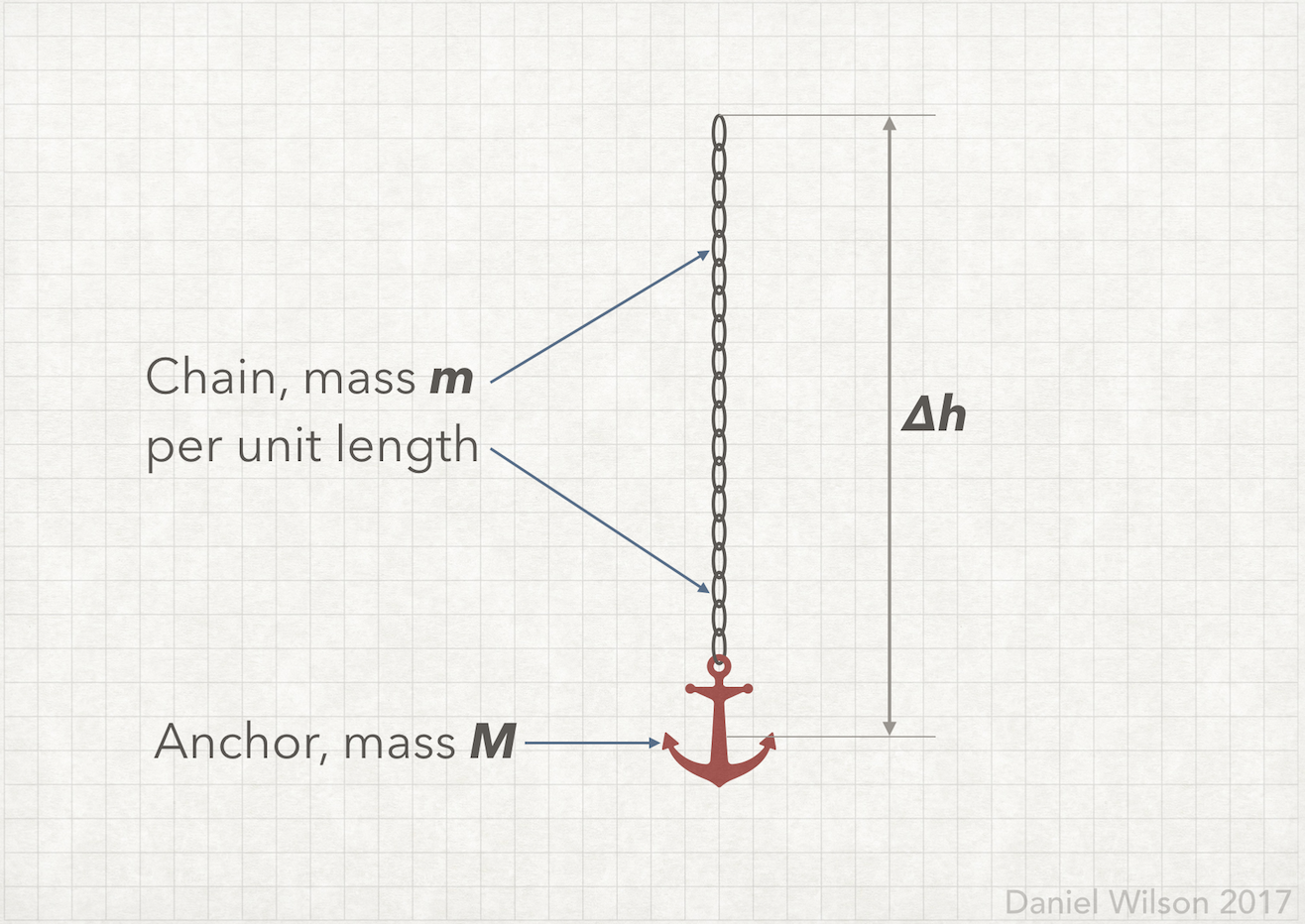
Height anchor moves through:
Mass of anchor:
Mass of chain per metre:
Work done is the integral of force with respect to the distance it is moved in the direction of the force. We need to establish the force as a function of the distance (height) it is moved through.
Since we are given the height it is moved through the integral is definite and the integration constant will cancel out. The anchor and chain are moved through a vertical height only and since the chain runs along that same height the force will be a linear function of the height.
The weight of the anchor that is moved through the height is a constant value since the mass is constant throughout. Whereas the mass of the chain is a function of the length of chain. Chain segments near the top move through less height than the chain segments near the bottom.
For the anchor:
The chain is made up of segments of weight each moving through a different height. The height each segment moves through is equal to the length of chain above. The force for each segment is the weight of each segment. The weight of the chain as a function of its length, r, is:
Where m is the mass per unit length and is a constant. The function is a linear function.
So our combined function for the force F in terms of r in the integral is:
Integrate the function
[See note below about this output of the integration.]
The work done raising the chain is a parabolic function. Final step…
That is the final answer, the work required to raise the anchor and chain is 22.3 kJ
Notice that the first term in the brackets is equal to the weight of the anchor (3,560 N) multiplied by the height (6.1 m) which is what we expected since the anchor has constant mass and simply rises through a vertical height of 6.1 m. So the work done to raise the anchor itself is simply weight multiplied by the height (W = Mg∆h which is the gravitational potential energy).

