Question #d04e8
1 Answer
The maximum is infinity. Notice on both sides of the graph, both as
Explanation:
First, a definition: We usually talk about extrema, not "extreme" when we look at polynomials. Extrema is just a fancy-sounding plural of extreme.
There is no straightforward way to factor or otherwise solve for the zeros of this polynomial algebraically. Enter it in your graphing calculator: 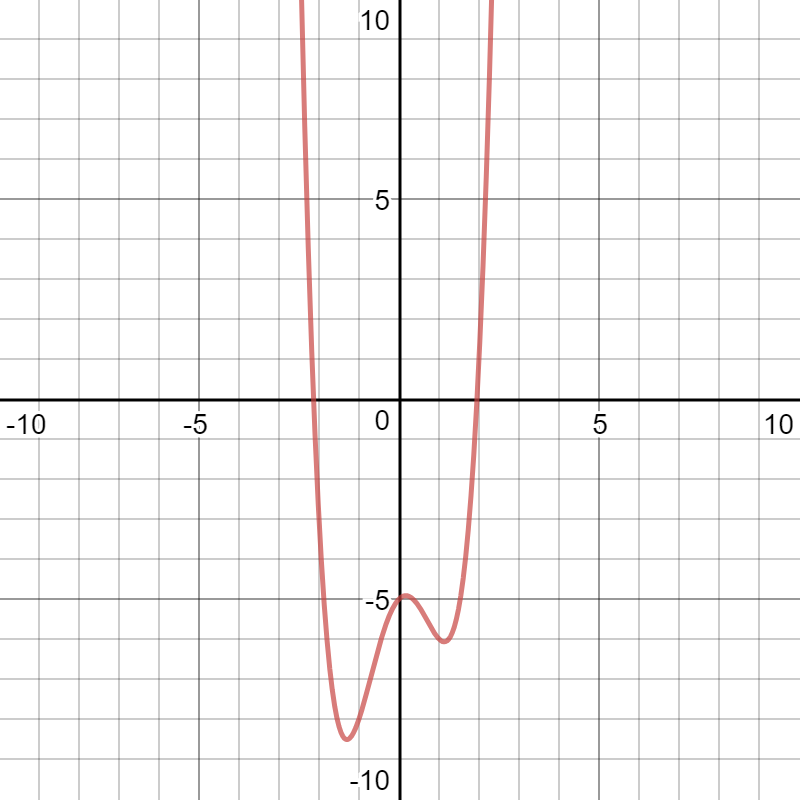
I know this is the whole graph because the graph of a fourth degree polynomial (where
Also, since the degree is an even number, both ends of the graph go in the same direction. Since
Your lower extrema are irrational, so finding them algebraically is not something we would normally do in pre-calculus.
Use the "minimum" function on your calculator to find the values.
If you have a TI-something, go into the "Calc" menu over the "Trace" button and choose "minimum". For "left bound", click somewhere the the left of the point you're looking for. For "right bound", click somewhere to the right. For "Guess", see how close you can get to the value. Don't worry if it's not very close! Your calculator knows.
The minima I get are at about
With your maxima at infinity, those are all the extrema of your polynomial.

