Question #b5dd9
2 Answers
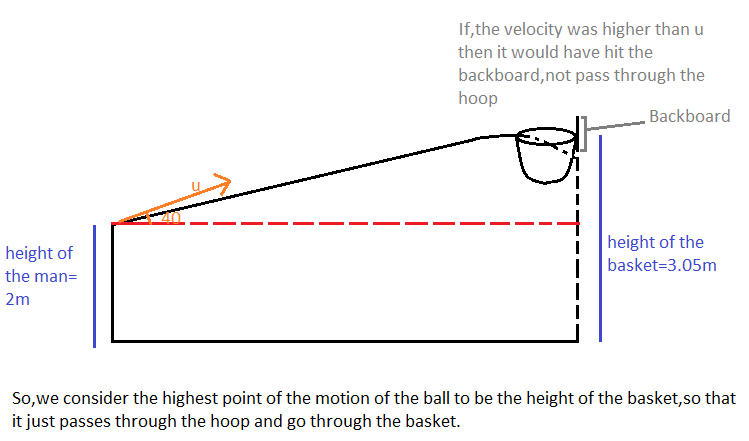
Suppose that the ball was thrown at
Now, considering vertical motion,it has to reach
So, we can use,
Where,
So,
Or,
The initial velocity is
Explanation:
Let 's have a rectangular coordinate system
Then the coordinates of the hoop are
Let the initial velocity of the ball is
The vertical component of the ball is
And
The horizontal component is
Substituting this value of
Let the acceleration due to gravity be
Plugging in the coordinates of the hoop
Solving for
graph{(y-0.839x+0.0735x^2)(y-1.05)=0 [1.31, 21.31, -1.11, 8.89]}


