Question

Question #5dc82

Answer 1

Here's what I got.

Explanation:

The first thing that you need to do here is to calculate the wavelength of the photon emitted when your electron undergoes a `n_i = 5 -> n_f = 2` transition in a hydrogen atom.

The wavelength of the photon will then help you determine its energy.

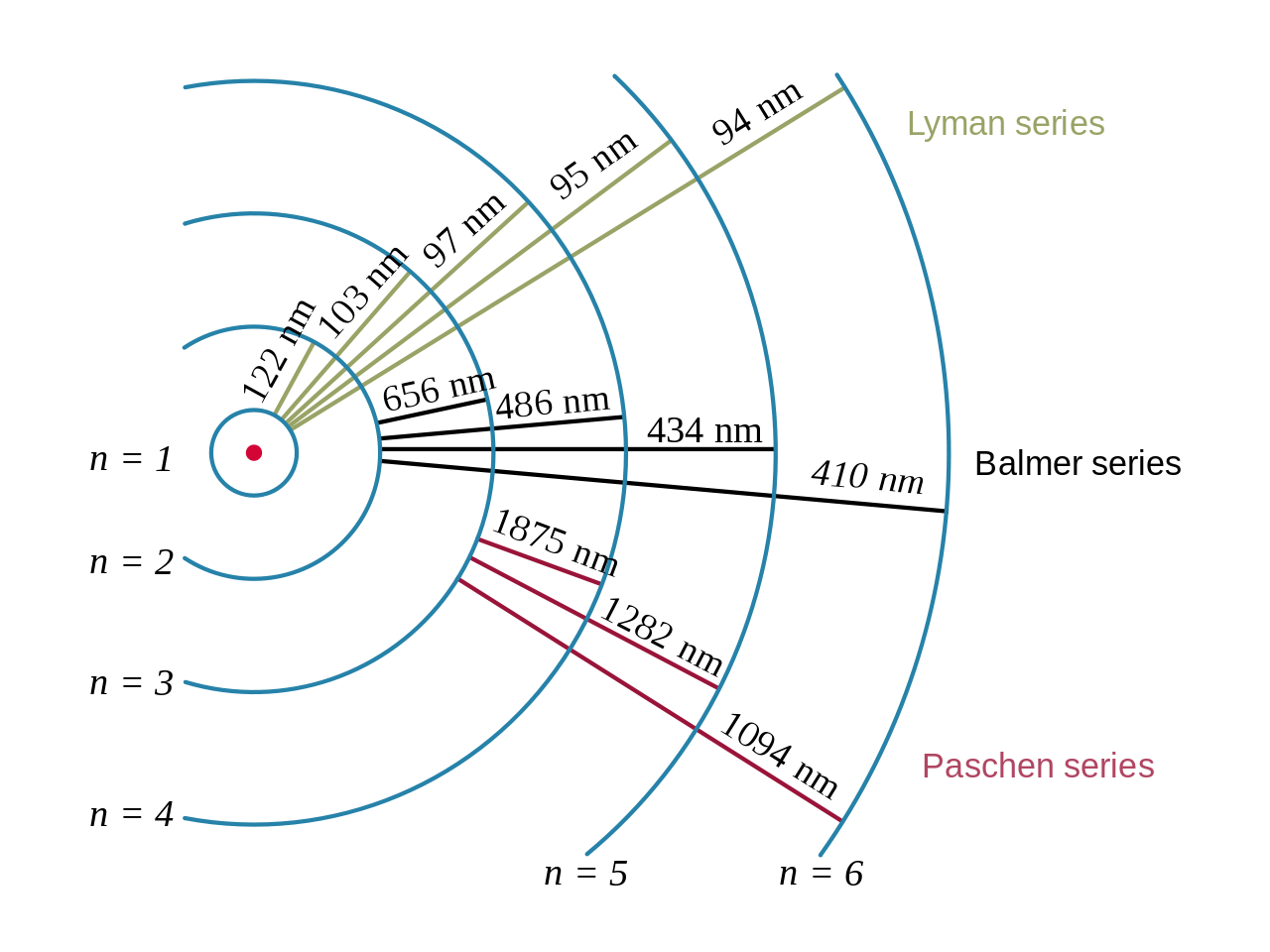
So, you know that when an electron in a hydrogen atom makes a transition from an initial energy level `n_i` to a final energy level `n_f`, it emits a photon whose wavelength is equal to

`1/(lamda) = R * (1/n_f^2 - 1/n_i^2)`

Here

• `R` is the Rydberg constant, equal to `1.097 * 10^(7)` `"m"^(-1)`

You can rearrange the above equation, which is called the Rydberg equation, as

`1/(lamda) = R * (n_i^2 - n_f^2)/(n_i^2 * n_f^2)`

which gets you

`lamda = 1/R * (n_i^2 * n_f^2)/(n_i^2 - n_f^2)`

In your case, you have `n_i = 5` and `n_f = 2`, which means that the emitted photon will have a wavelength of

`lamda = 1/(1.097 * 10^7color(white)(.)"m"^(-1)) * (5^2 * 2^2)/(5^2 - 2^2)`

`lamda = 4.34 * 10^(-7)color(white)(.)"m"`

Expressed in nanometers--recall that `"1 m" = 10^9` `"nm"`--the wavelength of the emitted photon will be

`lamda = color(darkgreen)(ul(color(black)("434 nm")))`

Now, in order to find the energy of the photon, you need to use a variation of the Planck - Einstein relation.

`E = h * c/(lamda)`

Here

• `E` is the energy of the photon
• `h` is Planck's constant, equal to `6.626 * 10^(-34)` `"J s"`
• `c` is the speed of light in a vacuum, usually given as `3 * 10^8` `"m s"^(-1)`

Plug in your value to find

`E = 6.626 * 10^(-34)"J" color(red)(cancel(color(black)("s"))) * (3 * 10^8 color(red)(cancel(color(black)("m"))) color(red)(cancel(color(black)("s"^(-1)))))/(4.34 * 10^(-7) color(red)(cancel(color(black)("m"))))`

`E = color(darkgreen)(ul(color(black)(4.58 * 10^(-19)color(white)(.)"J")))`

I'll leave both answers rounded to three sig figs.

It's worth mentioning that the `n_i = 5 -> n_f = 2` transition, which is part of the Balmer series, is located in the visible portion of the EM spectrum.